Bài 5: Cho hàm số: y = x4 + ax2 + b
a) Tính a, b để hàm số có cực trị bằng \({3 \over 2}\) khi x = 1
b) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho khi \(a = {{ – 1} \over 2},b = 1\)
c) Viết phương trình tiếp tuyến của (C) tại các điểm có tung độ bằng 1

Ta có: y’ = 4x3 + 2ax
a) Nếu hàm số có cực trị bằng \({3 \over 2}\) khi x = 1 thì:
\(\left\{ \matrix{
y'(1) = 0 \hfill \cr
y(1) = {3 \over 2} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
4 + 2a = 0 \hfill \cr
1 + a + b = {3 \over 2} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
a = – 2 \hfill \cr
b = {5 \over 2} \hfill \cr} \right.\)
b) Khi \(a = {{ – 1} \over 2},b = 1\) ta có hàm số: \(y = {x^4} – {1 \over 2}{x^2} + 1\)
_ Tập xác định: (-∞, +∞)
_ Sự biến thiên: y’ = 4x3 – x = x(4x2 – 1)
y’ = 0 ⇔ x = 0, \(x = \pm {1 \over 2}\)
Trên các khoảng \(({{ – 1} \over 2},0) \cup ({1 \over 2}, + \infty )\) , y’ > 0 nên hàm số đồng biến
Trên các khoảng \(( – \infty ,{{ – 1} \over 2}) \cup (0,{1 \over 2})\) , y’ < 0 nên hàm số nghịch biến
_ Cực trị: Hàm số đạt cực đại tại x = 0, yCD = 1
Hàm số đạt cực tiểu tại \(x = \pm {1 \over 2},{y_{CT}} = {{15} \over {16}}\)
Bảng biến thiên:
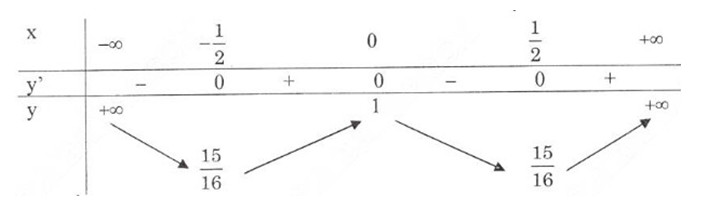
Đồ thị hàm số:
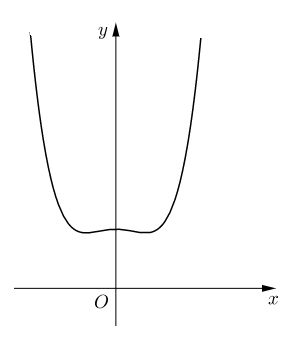
Đồ thị cắt trục tung tại điểm y = 1, không cắt trục hoành.
c) Với y = 1 ta có phương trình:
\({x^4} – {1 \over 2}{x^2} = 0 \Leftrightarrow x \in \left\{ {0, \pm {1 \over {\sqrt 2 }}} \right\}\)
Trên đồ thị có 2 điểm với tung độ bằng 1 là:
\({M_1}({{ – 1} \over {\sqrt 2 }},1);{M_2}(0,1);{M_3}({1 \over {\sqrt 2 }},1)\)
Ta lấy y’(0) = 0 nên tiếp tuyến với đồ thị tại M2 có phương trình là y = 1
Lại có:
\(y'({1 \over {\sqrt 2 }}) = {1 \over {\sqrt 2 }};y'({1 \over {\sqrt 2 }}) = {{ – 1} \over {\sqrt 2 }}\)
\(y = {{ – 1} \over {\sqrt 2 }}x + {1 \over 2} \Leftrightarrow y = {1 \over {\sqrt 2 }}x + {1 \over 2}\)
Bài 6: Cho hàm số \(y = {{x – 2} \over {x + m – 1}}\)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m = 2
b) Viết phương trình tiếp tuyến d của đồ thị (C) tại điểm có hoành độ a ≠ -1.

Advertisements (Quảng cáo)
a) Khi m = 2, ta có hàm số: \(y = {{x – 2} \over {x + 1}}\)
_ Tập xác định: (-∞, -1) ∪ (-1, +∞)
_ Sự biến thiên: \(y’ = {3 \over {{{(x + 1)}^2}}} > 0,\forall x \in ( – \infty , – 1) \cup (1, + \infty )\)
nên hàm số đồng biến trên hai khoảng này.
_ Hàm số không có cực trị
_ Giới hạn tại vô cực và tiệm cận ngang
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {{x – 2} \over {x + 1}} = 1;\mathop {\lim }\limits_{x \to – \infty } y = \mathop {\lim }\limits_{x \to – \infty } {{x – 2} \over {x + 1}} = 1\)
Nên x = -1 là tiệm cận đứng.
Bảng biến thiên:
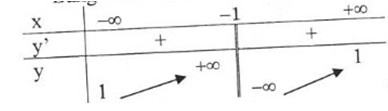
Đồ thị hàm số:
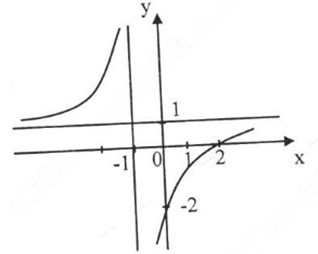
Đồ thị cắt trục tung tại y = -2, cắt trục hoành tại x = 2
b) Tiếp tuyến của đồ thị (C) tại điểm M có hoành độ a≠-1 có phương trình:
\(y = y'(a)(x – a) + y(a) = {3 \over {{{(a + 1)}^2}}}(x – a) + {{a – 2} \over {a + 1}}\)
Bài 7: Cho hàm số \(y = {2 \over {2 – x}}\)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
b) Tìm các giao điểm của (C) và đồ thị của hàm số y = x2 + 1. Viết phương trình tiếp tuyến của (C) tại mỗi giao điểm.
c) Tính thể tích vật thể tròn xoay thu được khi quay hình phẳng H giới hạn bởi đồ thị (C) và các đường thẳng y = 0, x = 0, x = 1 xung quanh trục Ox.

Advertisements (Quảng cáo)
a) _ Tập xác định: (-∞, 2) ∪(2, +∞)
_ Sự biến thiên: \(y’ = {2 \over {{{(2 – x)}^2}}} > 0,\forall x \in ( – \infty ,2) \cup (2, + \infty )\)
Nên hàm số đồng biến trên hai khoảng này.
_ Hàm số không có cực trị
_ Giới hạn tại vô cực và tiệm cận ngang
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {2 \over {2 – x}} = 0;\mathop {\lim }\limits_{x \to – \infty } y = \mathop {\lim }\limits_{x \to – \infty } {2 \over {2 – x}} = 0\)
Nên y = 0 là tiệm cận ngang.
_ Giới hạn vô cực và tiệm cận đứng:
\(\mathop {\lim }\limits_{x \to {2^ + }} y = \mathop {\lim }\limits_{x \to {2^ + }} ({2 \over {2 – x}}) = – \infty ;\mathop {\lim }\limits_{x \to {2^ – }} = \mathop {\lim }\limits_{x \to {2^ – }} ({2 \over {2 – x}}) = + \infty \)
Nên x = 2 là tiệm cận đứng.
_ Bảng biến thiên:
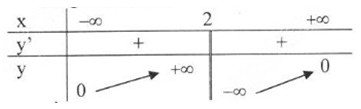
Đồ thị hàm số:
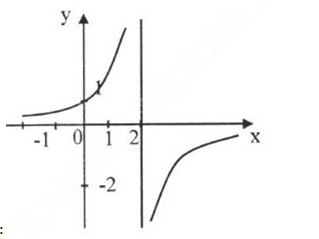
Đồ thị hàm số:
Đồ thị cắt trục tung tại y = 1, không cắt trục hoành.
b) Phương trình xác định hoành độ giao điểm:
\({2 \over {2 – x}} = {x^2} + 1 \Leftrightarrow {x^3} – 2{x^2} + x = 0 \Leftrightarrow x \in \left\{ {0,1} \right\}\)
Hai đồ thị cắt nhau tại hai điểm M1 (0, 1), M2(1, 2)
Tiếp tuyến với đồ thị (C): \(y = {2 \over {2 – x}}\) tại điểm M1 có phương trình là: \(y = {1 \over 2}x + 1\)
Tiếp tuyến tại điểm M2 có phương trình y = 2(x – 1) + 2 = 2x
c) Trong khoảng (0, 1) đồ thị (C) nằm phía trên trục hoành nên thể tích cần tính là :
\(V = \pi \int_0^1 {({2 \over {2 – x}}} {)^2} = 2\pi \)
Bài 8: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) \(f(x) = 2x^3– 3x^2– 12x + 1\) trên đoạn \(\left[ { – 2,{5 \over 2}} \right]\)
b) \( f(x) = x^2lnx\) trên đoạn \(\left[ {1,e} \right]\)
c) \(f(x) = xe^{-x}\) trên nửa khoảng \([0, +∞)\)
d) \(f(x) = 2sinx + sin2x\) trên đoạn \(\left[ {0,{{3\pi } \over 2}} \right]\)

a) \(f(x) = 2x^3– 3x^2– 12x + 1 ⇒ f’(x) = 6x^2 – 6x – 12\)
\(f’(x) = 0 ⇔ x =-1\) hoặc \(x=2\)
So sánh các giá trị:
\(f(-2) = -3\); \( f(-1) = 8\);
\(f(2) = -19\), \(f({5 \over 2}) = {{ – 33} \over 2}\)
Suy ra:
\(\eqalign{
& \mathop {\max }\limits_{x \in \left[ { – 2,{5 \over 2}} \right]} f(x) = f( – 1) = 8 \cr
& \mathop {min}\limits_{x \in \left[ { – 2,{5 \over 2}} \right]} f(x) = f(2) = – 19 \cr} \)
b) \(f(x) = x^2 lnx ⇒ f’(x)= 2xlnx + x > 0, ∀ x ∈ [1, e]\) nên \(f(x)\) đồng biến.
Do đó:
\(\eqalign{
& \mathop {\max }\limits_{x \in \left[ {1,e} \right]} f(x) = f(e) = {e^2} \cr
& \mathop {min}\limits_{x \in \left[ {1,e} \right]} f(x) = f(1) = 0 \cr} \)
c) \(f(x)= xe^{-x}⇒ f’(x)=e^{-x} –xe^{-x} = (1 – x)e^{-x}\) nên:
\(f’(x) = 0 ⇔ x = 1, f’(x) > 0, ∀x ∈ (0, 1)\) và \(f’(x) < 0, ∀x ∈ (1, +∞)\)
nên:
\(\mathop {\max }\limits_{x \in {\rm{[}}0, + \infty )} f(x) = f(1) = {1 \over e}\)
Ngoài ra \(f(x)= xe^{-x} > 0, ∀ x ∈ (0, +∞)\) và \(f(0) = 0\) suy ra
\(\mathop {\min}\limits_{x \in {\rm{[}}0, + \infty )} f(x) = f(0) = 0\)
d) \(f(x) = 2sinx + sin2x ⇒ f’(x)= 2cosx + 2cos2x\)
\(f’(x) = 0 ⇔ cos 2x = -cosx ⇔ 2x = ± (π – x) + k2π\)
⇔ \(x \in \left\{ { – \pi + k2\pi ;{\pi \over 3} + {{k2\pi } \over 3}} \right\}\)
Trong khoảng \(\left[ {0,{{3\pi } \over 2}} \right]\) , phương trình \(f’(x) = 0\) chỉ có hai nghiệm là \({x_1} = {\pi \over 3};{x_2} = \pi \)
So sánh bốn giá trị : \(f(0) = 0\); \(f({\pi \over 3}) = {{3\sqrt 3 } \over 2};f(\pi ) = 0;f({{3\pi } \over 2}) = – 2\)
Suy ra:
\(\eqalign{
& \mathop {\max }\limits_{x \in \left[ {0,{{3\pi } \over 2}} \right]} f(x) = f({\pi \over 3}) = {{3\sqrt 3 } \over 2} \cr
& \mathop {min}\limits_{x \in \left[ {0,{{3\pi } \over 2}} \right]} f(x) = f({{3\pi } \over 2}) = – 2 \cr} \)

