Câu I.4: Cho hình bình hành ABCD có \(\widehat A = 120^\circ \), AB = a, BC = b. Các đường phân giác của bốn góc A, B, C, D cắt nhau tạo thành tứ giác MNPQ. Tính diện tích tứ giác MNPQ.

(h.bs.21).
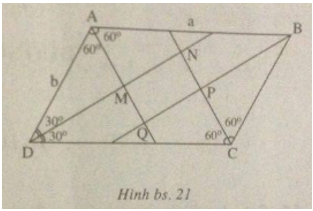
Đường phân giác của góc A cắt đường phân giác của góc D tại M thì tam giác ADM có hai góc bằng
60º và 30º nên các đường phân giác đó vuông góc với nhau. Lập luận đó chứng tỏ hình MNPQ có 4 góc vuông nên MNPQ là hình chữ nhật.
Trong tam giác vuông ADM có \(DM = AD\sin \widehat {DAM} = b\sin 60^\circ = {{b\sqrt 3 } \over 2}.\)
Advertisements (Quảng cáo)
Trong tam giác vuông DCN ( N là giao của đường phân giác góc D và đường phân giác góc C) có \(DN = DC\sin \widehat {DCN}{\rm{ = asin60}}^\circ {\rm{ = }}{{a\sqrt 3 } \over 2}.\)
Vậy \(MN = DN – DM = (a – b){{\sqrt 3 } \over 2}.\)
Trong tam giác vuông DCN có \(CN = CD\cos 60^\circ = {a \over 2}.\) Trong tam giác vuông BCP ( P là giao của đường phân giác góc C với đường phân giác góc B) có \(CP = CB\cos 60^\circ = {b \over 2}.\)
Vậy: \(NP = CN – CP = {{a – b} \over 2}.\)
Advertisements (Quảng cáo)
Suy ra diện tích hình chữ nhật MNPQ là
\(MN \times NP = {(a – b)^2}{{\sqrt 3 } \over 4}\)
Câu I.5: Cho tam giác ABC vuông tại C có \(\widehat B = 37^\circ \). Gọi I là giao điểm của cạnh BC với đường trung trực của AB. Hãy tính AB, AC, nếu biết BI = 20.

(h.bs.22).
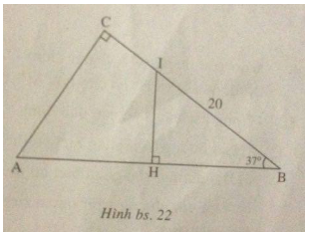
Gọi H là trung điểm của AB thì trong tam giác vuông HBI, ta có HB = IBcosB nên AB = 2HB = 2IB cosB = 40cos37º \( \approx \) 31,95.

