Câu 29. Trong các mệnh đề sau, mệnh đề nào đúng ?
a. Hai mặt phẳng phân biệt cùng song song với một đường thẳng thì song song với nhau
b. Hai mặt phẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau
c. Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trên một mặt phẳng đều song song với mặt phẳng còn lại.
d. Nếu hai mặt phẳng song song thì mỗi đường thẳng nằm trên một mặt phẳng này đều song song với mọi đường thẳng nằm trên mặt phẳng kia.
e. Nếu hai mặt phẳng phân biệt lần lượt đi qua hai đường thẳng song song thì song song với nhau.
f. Nếu một đường thẳng cắt một trong hai mặt phẳng song song thì cắt mặt phẳng còn lại.
a. Sai vì hai mặt phẳng có thể cắt nhau theo giao tuyến song song với đường thẳng đã cho.
b. Đúng
c. Đúng
d. Sai
e. Sai vì có thể hai mặt phẳng cắt nhau.
f. Đúng
Câu 30. Trong các mệnh đề sau, mệnh đề nào đúng?
a. Hình hộp là một hình lăng trụ
b. Hình lăng trụ có tất cả các cạnh song song
c. Hình lăng trụ có tất cả các mặt bên bằng nhau
d. Hình lăng trụ có các mặt bên là hình bình hành
e. Hình hộp có các mặt đối diện bằng nhau
a. Đúng
b. Sai vì cạnh đáy không song song với cạnh bên.
c. Sai
d. Đúng
e. Đúng
Câu 31. Cho hai đường thẳng chéo nhau. Chứng minh rằng có đúng hai mặt phẳng song song với nhau lần lượt đi qua hai đường thẳng đó
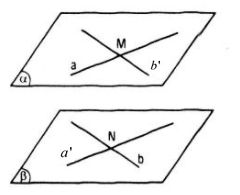
Gọi hai đường thẳng chéo nhau là a và b.
Trên đường thẳng a, ta lấy điểm M, qua M kẻ đường thẳng b’ // b
Trên đường thẳng b, ta lấy điểm N, qua N ta kẻ đường thẳng a’ // a
Gọi (α) = mp(a, b’), (β) = mp(b, a’) thì (α) // (β)
* Ta chứng tỏ cặp mặt phẳng (α), (β) là duy nhất.
Thật vậy, giả sử tồn tại cặp (α’) , (β’) sao cho (α’) chứa a, (β’) chứa b và \((α’) // (β’)\). Ta chứng minh \((α’) ≡ (α)\) và \((β’) ≡ (β)\) .
– Do (α’) và (α) cùng chứa a, nên nếu (α’) và (α) không trùng nhau thì \((α’) ∩ (α) = a\) (1)
– Do \( (α’) // (β’) ⇒ b // (α’)\) (2)
– Do \((α) // (β) ⇒ b // (α)\) (3)
Từ (1), (2) và (3) suy ra a // b, mâu thuẫn giả thiết
Vậy \((α) ≡ (α’)\), tương tự \((β) ≡ (β’)\)
Do đó cặp mặt phẳng \((α), (β)\) duy nhất.
Câu 32. Cho hai đường thẳng chéo nhau a và b lần lượt nằm trên hai mặt phẳng song song (P) và (Q). Chứng minh rằng nếu điểm M không nằm trên (P) và không nằm trên (Q) thì có duy nhất một đường thẳng đi qua M cắt cả a và b
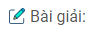
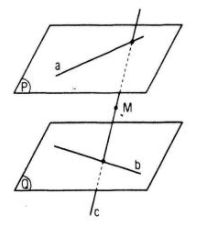
Giả sử c = mp ( M, a) ∩ mp(M, b). Ta cần chứng minh c cắt cả a và b.
Vì c và a cũng nằm trên một mặt phẳng và không thể trùng nhau ( do c qua M và a không đi qua M) nên hoặc c // a hoặc c cắt a. Cũng vậy, hoặc c // b hoặc c cắt b.
Không thể xảy ra đồng thời c // a; c // b vì a và b chéo nhau. Vậy nếu c song song với a và c phải cắt b, tức là c qua một điểm của mp (Q) và song song với a, suy ra c phải thuộc mp (Q), và do đó M thuộc (Q) (trái giả thiết).
Tương tự, không thể có c song song với b.
Tóm lại c cắt a và b.
Nếu còn có đường thẳng c’ khác c đi qua M, cắt cả a và b thì a và b đồng phẳng. Vô lí.

Advertisements (Quảng cáo)
Câu 33. Trong mặt phẳng (P) cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường thẳng a, b, c, d đôi một song song với nhau và không nằm trên (P). Một mặt phẳng cắt a, b, c, d lần lượt tại bốn điểm A’, B’, C’, D’. Chứng minh rằng A’B’C’D’ là hình bình hành
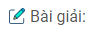
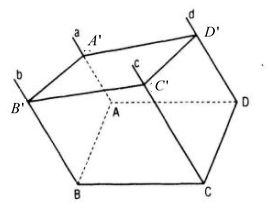
Ta có: \(\left\{ {\matrix{ {a//b} \cr {AD//BC } \cr {a \cap AD=A } \cr } } \right.\Rightarrow \left( {a,d} \right)//\left( {b,c} \right) \)
Tương tự (a, b) // (c, d).
Vì hai mặt phẳng (a, b) và (c, d) song song nhau nên mp(A’B’C’) cắt hai mặt phẳng này
lần lượt theo hai giao tuyến A’B’ và C’D’ song song nhau.
Tương tự A’D’// B’C’.
Vậy A’B’C’D’ là hình bình hành.
Câu 34. Cho tứ diện ABCD. Gọi M là trung điểm của AB. Hỏi mặt phẳng (P) qua điểm M, song song với cả AD và BC có đi qua trung điểm N của CD không ? Tại sao ?
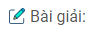
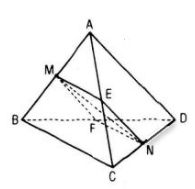
Giả sử (P) cắt BD, AC và CD lần lượt tại F, E, N. Vì AD // (P) nên (P) cắt mp(ABD) theo giao tuyến MF // AD.
Vì M là trung điểm của AB nên F là trung điểm của BD.
Vì BC // (P) nên (P) cắt mp(BCD) theo giao tuyến FN // BC. Vì F là trung điểm của BD nên N là trung điểm của CD.
Câu 35. Cho hai điểm M, N lần lượt thay đổi trên hai mặt phẳng song song (P) và (Q). Tìm tập hợp các điểm I thuộc đoạn thẳng MN sao cho \({{IM} \over {IN}} = k,k \ne 0\)cho trước
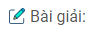
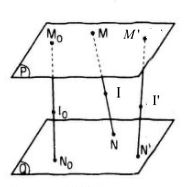
Thuận. Giả sử M \(\in\) (P), N \(\in\) (Q) và điểm I thuộc đoạn thẳng MN sao cho \({{IM} \over {IN}} = k.\)
Trên hai mặt phẳng (P) và (Q), ta lần lượt lấy hai điểm cố định M0 và N0 rồi lấy một điểm I0 thuộc đoạn thẳng M0N0 sao cho \({{{M_0}{I_0}} \over {{N_0}{I_0}}} = k.\) Khi ấy điểm I0 cố định.
Ta có: \({{IM} \over {IN}} = {{{I_0}{M_0}} \over {{I_0}{N_0}}}\left( { = k} \right)\)
\(\Rightarrow {{IM} \over {{I_0}{M_0}}} = {{IN} \over {{I_0}{N_0}}} = {{IM + IN} \over {{I_0}{M_0} + {I_0}{N_0}}} = {{MN} \over {{M_0}{N_0}}}\)
Áp dụng định lí Ta-lét đảo, ta suy ra đường thẳng I0I thuộc một mặt phẳng (R) song song với (P) và (Q). Mặt phẳng (R) cố định vì nó qua điểm cố định I0 và song song với mặt phẳng cố định (P). Vậy điểm I thuộc mặt phẳng (R) cố định.
Đảo. Ngược lại, lấy một điểm I’ bất kì trên mặt phẳng (R). Qua I’ ta kẻ một đường thẳng cắt hai mặt phẳng (P) và (Q) lần lượt tại M’ và N’. Xét hai cát tuyến M0N0 , M’N’ và ba mặt phẳng song song (P), (Q), (R).
Theo định lí Ta-lét ta có: \({{I’M’} \over {{I_0}{M_0}}} = {{I’N’} \over {{I_0}{N_0}}} = {{M’N’} \over {{M_0}{N_0}}}\)
Từ đó, ta suy ra I thuộc đoạn thẳng M’N’ và \({{I’M’} \over {I’N’}} = {{{I_0}{M_0}} \over {{I_0}{N_0}}} = k\)
Kết luận: Tập hợp điểm I thuộc đoạn thẳng MN sao cho \({{IM} \over {IN}} = k\) là mặt phẳng (R) nói trên.
Câu 36. Cho hình lăng trụ đứng tam giác ABC.A’B’C’. Gọi H là trung điểm của cạnh A’B’.
a. Chứng minh rằng đường thẳng CB’ song song với mp(AHC’)
b. Tìm giao tuyến d của hai mặt phẳng (AB’C’) và (A’BC). Chứng minh rằng d song song với mp(BB’C’C)
c. Xác định thiết diện của hình lăng trụ ABC.A’B’C’ khi cắt bởi mp(H , d)
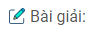
Advertisements (Quảng cáo)
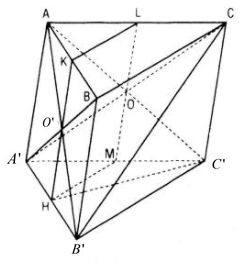
a) Chứng minh CB’ // (AHC’)
Ta tìm trong (AHC’) một đường thẳng song song với CB’, muốn vậy ta tìm giao tuyến của một mặt phẳng chứa CB’ với (AHC’), đó là (A’CB’).
Gọi O là giao điểm AC’ và A’C.
AA’C’C là hình bình hành nên O là trung điểm của A’C.
Do đó HO là đường trung bình của ∆A’B’C
⇒ HO // B’C ⇒ B’C // (AHC’). ( vì HO \(\subset\) (AHC’)).
b) Tìm giao tuyến d của (AB’C’) và (A’BC).
Gọi O’ là giao điểm của AB’ và A’B thì O, O’ là hai điểm chung của hai mặt phẳng (AB’C’) và (A’BC) nên (AB’C’) ∩ (A’BC) = OO’
Vậy d = OO’. Ta có O’ là trung điểm của AB’ ( vì AA’B’B là hình bình hành).
⇒ OO’ là đường trung bình của ∆AB’C’.
⇒ OO’ // B’C’ // BC ⇒ OO’ // (BB’C’C) ⇒ d // (BB’C’C)
c) Gọi {K} = HO’ ∩ AB thì HK // AA’
Qua O kẻ ML // AA’ ( M ∈ A’C’, L ∈ AC).
Thiết diện cần tìm là hình bình hành HKLM.
Câu 37. Cho hình hộp ABCD.A’B’C’D’. Chứng minh rẳng
a. mp(BDA’) // mp(B’D’C)
b.Đường chéo AC’ đi qua các trọng tâm G1, G2 của hai tam giác BDA’ và B’D’C
c. G1 và G2 chia đoạn AC’ thành ba phần bằng nhau
d. Các trung điểm của sáu cạnh BC, CD, DD’, D’A’, A’B’,B’B cùng nằm trên một mặt phẳng
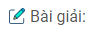
a) Chứng minh ( BDA’) // (B’D’C)
Ta có tứ giác BB’D’D và A’B’CD là các hình bình hành nên : BD // B’D’ và DA’ // B’C
⇒ hai mặt phẳng (BDA’) và (B’D’C) có các cặp đường thẳng cắt nhau và song song nhau từng đôi một nên chúng song song.
Vậy (BDA’) // (B’D’C).
b) Chứng minh G1 , G2 ∈ AC’
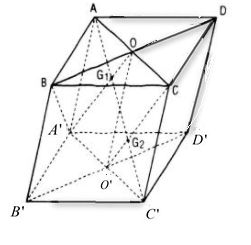
Gọi O, O’ lần lượt là tâm của hình bình hành ABCD và A’B’C’D’.
Trong mặt phẳng (AA’C’C) gọi G1 , G2 lần lượt là giao điểm của AC’ với A’O và O’C. Ta chứng minh G1, G2 lần lượt là trong tâm của ∆A’BD và ∆CB’D’.
Thật vậy, ta có ∆G1OA đồng dạng ∆G1A’C’ ( vì AC // A’C’)
\( \Rightarrow {{{G_1}O} \over {{G_1}A’}} = {{OA} \over {A’C’}} = {1 \over 2} \Rightarrow {{A'{G_1}} \over {A’O}} = {2 \over 3}\)
⇒ G1 là trọng tâm ∆A’BD.
Tương tự, G2 là trọng tâm ∆CB’D’. Vậy AC’ đi qua G1, G2 .
c) Chứng minh AG1 = G1G2 = G2C’
Theo câu trên , ta có:
\({{A{G_1}} \over {{G_1}C’}} = {{AO} \over {A’C’}} = {1 \over 2}\) ( vì ∆G1OA đồng dạng ∆G1A’C’) \( \Rightarrow A{G_1} = {1 \over 3}AC’\) (1)
Tương tự: \({{C'{G_2}} \over {{G_2}A}} = {{C’O’} \over {CA}} = {1 \over 2}\) ( vì ∆G2C’O’ đồng dạng ∆G2AC) \( \Rightarrow C'{G_2} = {1 \over 3}AC’\) (2)
Từ (1) và (2) suy ra: AG1 = G1G2 = G2C’.
d)
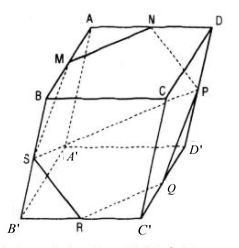
Gọi M, N, P, Q, S, R lần lượt là trung điểm của các cạnh AB, AD, DD’, C’D’, C’B’, B’B.
Ta có: \(\left\{ {\matrix{ {MN//BD} \cr {SP//BD} \cr } } \right. \Rightarrow MN//SP\)
Gọi (α) = (MN, SP)
Ta có : \(\left\{ {\matrix{ {PQ//DC’} \cr {MS//AB’} \cr } } \right. \Rightarrow PQ//MS\)
( vì DC’ // AB’)
⇒ PQ ⊂ (α) do đó Q ∈ (α).
Tương tự: QR // MN ⇒ QR ⊂ (α) do đó R ∈ (α).
Vậy M, N, P, Q, R, S ∈ (α).
Mặt khác vì \(\left\{ {\matrix{ {MS//AB’} \cr {NP//AD’} \cr } } \right.\) nên (MNPQRS) // (AB’D’).
Câu 38. Chứng minh rẳng tổng bình phương tất cả các đường chéo của một hình hộp bằng tổng bình phương tất cả các cạnh của hình hộp đó
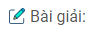
Áp dụng tính chất: “ Trong một hình bình hành, tổng bình phương hai đường chéo bằng tổng bình phương bốn cạnh.”
Đặt AB = a, BC = b, AA’ = c ( đó là 3 kích thước của hình hộp).
Trong hình bình hành ABC’D’ ta có:
\(AC'{^2} + BD{‘^2} = 2\left( {{a^2} + BC'{^2}} \right)\) (1)
Trong hình bình hành A’B’CD ta có:
\(A'{C^2} + B'{D^2} = 2\left( {{a^2} + B'{C^2}} \right)\) (2)
Cộng (1) và (2) ta được :
\(AC'{^2} + BD'{^2}+A'{C^2} + B'{D^2} = 2\left( {2{a^2} + BC{‘^2} + B'{C^2}} \right)\) (3)
Mặt khác trong hình bình hành BB’C’C ta có:
\(BC{‘^2} + B'{C^2} = 2\left( {{b^2} + {c^2}} \right)\) (4)
Thay (4) vào (3) ta được :
\(AC'{^2} + BD'{^2} + A'{C^2} + B\,'{D^2} = 4\left( {{a^2} + {b^2} + {c^2}} \right)\) (đpcm).
Câu 39. Cho hình chóp cụt ABC.A’B’C’ có đáy lớn ABC và các cạnh bên AA’, BB’, CC’. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA và M’, N’, P’ lần lượt là trung điểm của các cạnh A’B’, B’C’, C’A’. Chứng minh MNP.M’N’P’ là hình chóp cụt
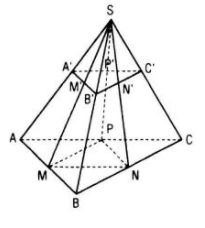
Gọi S là giao điểm các cạnh bên AA’, BB’, CC’của hình chóp cụt.
Do A’B’ // AB và M’, M lần lượt là trung điểm của A’B’, AB nên MM’ đi qua S.
Tương tự NN’, PP’ cùng đi qua S.
Vậy MM’, NN’, PP’ đồng quy tại S.
Ta có (M’N’P’) // (MNP) nên MNP.M’N’P’ là hình chóp cụt.

