Bài 14: Chứng minh rằng các tiếp tuyến của mặt cầu song song với một đường thẳng cố định luôn nằm trên một mặt trụ xác định.
Giải
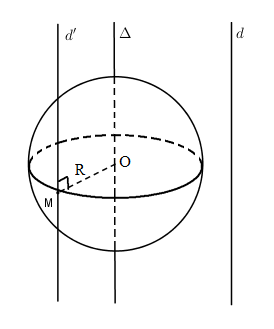
Cho mặt cầu \(S(O;R)\) và đường thẳng \(d\).
Gọi \(\Delta \) là đường thẳng đi qua \(O\) và song song với \(d\). Nếu \(d’\) là tiếp tuyến của mặt cầu và \(d’ // d\) thì \(d’\) cách \(\Delta \) một khoảng không đổi \(R\). Vậy \(d’\) nằm trên mặt trụ có trục \(\Delta \) và có bán kính bằng \(R\).
Bài 15: Mặt phẳng đi qua trục của một hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh \(2R\).
a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.
b) Tính thể tích của khối trụ.
c) Tính thể tích của khối lăng trụ tứ giác đều nội tiếp hình trụ.
Giải
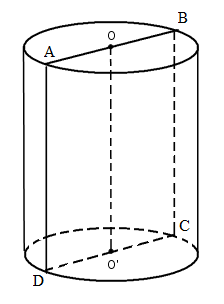
Mặt phẳng đi qua \(OO’\) của hình trụ, cắt hình trụ theo thiết diện là hình vuông \(ABCD\) cạnh \(2R\), do đó bán kính đáy bằng \(R\) và đường sinh \(AD = 2R\).
Advertisements (Quảng cáo)
a) Ta có:
\(\eqalign{
& {S_{xq}} = 2\pi .R.2R = 4\pi {R^2} \cr
& {S_{tp}} = {S_{xq}} + 2{S_{day}} = 4\pi {R^2} + 2\pi {R^2} = 6\pi {R^2} \cr} \)
b) Thể tích của khối trụ là \(V = \pi {R^2}.2R = 2\pi {R^3}\).
c) Hình lăng trụ tứ giác đều nội tiếp hình trụ là hình lăng trụ đứng có cạnh bên bằng \(2R\) và có đáy là hình vuông cạnh \(R\sqrt 2 \) nên có thể tích \({V_{LT}} = 2{R^2}.2R = 4{R^3}\).
Bài 16: Một hình trụ có bán kính đáy bằng \(R\) và chiều cao \(R\sqrt 3 \).
a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.
b) Tình thể tích của khối trụ giới hạn bởi hình trụ.
Advertisements (Quảng cáo)
c) Cho hai điểm A và B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng \({30^0}\). Tính khoảng cách giữa AB và trục của hình trụ.
Giải
a) Diện tích xung quanh của hình trụ
\({S_{xq}} = 2\pi R.R\sqrt 3 = 2\sqrt 3 \pi {R^2}\)
Diện tích toàn phần của hình trụ là:
\({S_{tp}} = {S_{xq}} + 2{S_{day}} = 2\sqrt 3 \pi {R^2} + 2\pi {R^2}\)
\(= 2\left( {\sqrt 3 + 1} \right)\pi {R^2}\)
b) Thể tích của khối trụ \(V = \pi {R^2}.R\sqrt 3 = \sqrt 3 \pi {R^3}\).
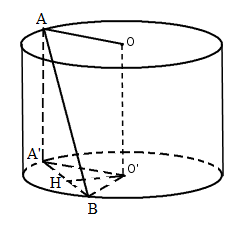
c) Gọi \(O\) và \(O’\) là tâm của hao đường tròn đáy.
Kẻ \(AA’ // OO’\) (A’ nằm trên đáy dưới hình trụ)
Ta có: \(O’A’ = R\,\,,\,\,AA’ = R\sqrt 3 \) và \(\widehat {BAA’} = {30^0}\).
Vì \(OO’ // (ABA’)\) nên khoảng cách giữa \(OO’\) và \(AB\) bằng khoảng cách giữa \(OO’\) và \((ABA’)\).
Kẻ \(OH \bot A’B\) thì \(H\) là trung điểm của \(A’B\) (quan hệ vuông góc giữa đường kính và dây cung) và \(O’H \bot \left( {ABA’} \right)\).
Trong tam giác vuông \(AA’B\) ta có:
\(\tan {30^0} = {{AB’} \over {AA’}} \Rightarrow AB’ = AA’.tan{30^0} \)
\(= R\sqrt 3 .{1 \over {\sqrt 3 }} = R\)
Vậy tam giác \(BA’O’\) là tam giác đều cạnh \(R\) nên \(O’H = {{R\sqrt 3 } \over 2}\).

