Bài 44-45.1: Đặt một điểm sáng S nằm trước thấu kính phân kì như hình 44-45.1
a. Dựng ảnh S’ của S tạo bởi kính đã cho.
b. S’ là ảnh thật hay ảnh ảo ? Vì sao ?
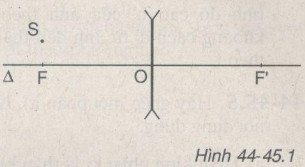
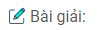
a) Hình dưới đây:
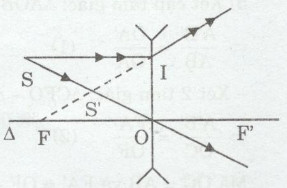
b) S’ là ảnh ảo vì nó là giao điểm của các tia ló kéo dài.
Bài 44-45.2: Hình 44-45.2 vẽ trục chính Δ của một thấu kính, S là một điểm sáng, S’ là ảnh của S.
a. Hãy cho biết S’ là ảnh thật hay ảnh ảo ?
b. Thấu kính đã cho là thấu kính hội tụ hay phân kì ?
c. Bằng cách vẽ hãy xác định quang tâm O, tiêu điểm F, F’ của thấu kính đã cho.
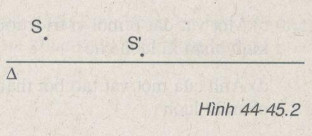
a) S’ là ảnh ảo vì S’ và S cùng nằm một phía đối với trục chính của thấu kính.
b) Thấu kính đem dùng là thấu kính phân kì.
Advertisements (Quảng cáo)
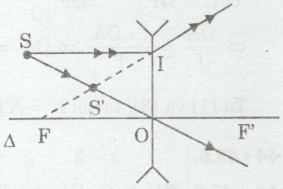
c) Cách xác định tâm O, F, F’ của thấu kính:
– Nối S và S’ cắt trục chính của thấu kính tại O.
– Dựng đường thẳng vuông góc với trục chính tại O. Đó là vị trí đặt thấu kính.
– Từ S dựng tia tới SI song song với trục chinh của thấu kính. Nối I với S’ cắt trục chính tại tiêu điểm F, lấy OF = OF’.
Bài 44-45.3: Trên hình 44-45.3 có vẽ trục chính Δ, quang tâm O, hai tiêu điểm F, F’ của một thấu kính, hai tia ló 1, 2 của hai tia tới xuất phát từ một điểm sáng S.
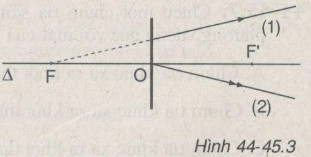
a. Thấu kính đã cho là thấu kính hội tụ hay phân kì ?
b. Bằng cách vẽ hãy xác định ảnh S’ và điểm sáng S.
Advertisements (Quảng cáo)
a) Thấu kính đem dùng là thấu kính phân kì.
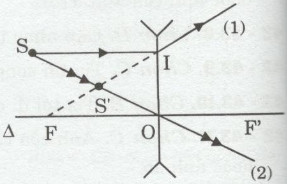
b) Phương pháp xác định S và S’:
– Xác định ảnh S’: Kéo dài tia ló số 2, cắt đường kéo dài của tia ló 1 tại đâu thì đó là S’.
– Xác định điểm S: Vì tia ló số 1 kéo dài đi qua tiêu điểm F nên tia tới của nó phải đi song song với trục chính của thấu kính. Tia này cắt tia kia qua quang tâm ở đâu thì đó là điểm sáng S.
Bài 44-45.4: Vật sáng AB có độ cao h được đặt vuông góc với trục chính của một thấu kính phân kì tiêu cự f. Điểm A nằm trên trục chính và có vị trí tại tiêu điểm F (hình 44-45.4).
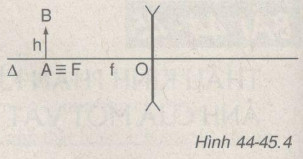
a. Dựng ảnh A’B’ của AB qua thấu kính đã cho.
b. Vận dụng kiến thức hình học hãy tính độ cao h’ của ảnh theo h và khỏang cách d’ từ ảnh đến thấu kính theo f.
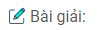
a) Dựng ảnh A’B’ của AB qua thấu kính phân kì.
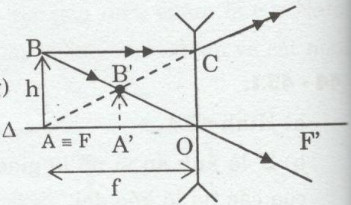
b) Xét cặp tam giác: AAOB ~ AA’OB’ (g-g)
\( \Rightarrow {{A’B’} \over {AB}} = {{OA’} \over {OA}}\) (1)
– Xét 2 tam giác ∆CFO ~∆B’FA’ (g-g)
\( \Rightarrow {{A’B’} \over {OC}} = {{FA’} \over {OF}}\) (2)
Mà OC = AB và FA’ = OF – OA’
Từ (1) và (2) ta có:
\({{OA’} \over {OA}} = {{F{\rm{A}}’} \over {OF}} = {{OF – OA’} \over {OF}}(d = OA = OF = f)\)
\(\eqalign{
& \Leftrightarrow {{OA’} \over f} = {{f – OA’} \over f} \cr
& \Rightarrow OA’ = f – OA’ \cr
& \Rightarrow 20A’ = f \cr
& \Rightarrow d’ = OA’ = {f \over 2}\,\,\,\,\left( 3 \right) \cr} \)
Từ (1) và (3), ta có: \(h’ = A’B’ = {{f.h} \over {2f}} = {h \over 2} \Rightarrow h’ = {h \over 2}\)

