Bài 1: Trong bảng phân tích dao động theo từng thời điểm trên Hình 21.3, ta có :
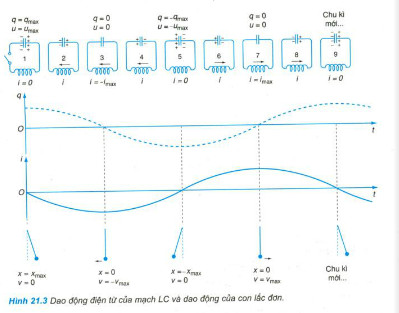
A. Năng lượng điện trường cực đại tại thời điểm số 2.
B. Năng lượng từ trường cực đại tại thời điểm số 4.
C. Năng lượng điện trường cực đại tại thời điểm số 6.
D. Năng lượng từ trường cực đại tại thời điểm số 7.
Giải
Ta có năng lượng từ trường cực đại tại thời điểm số 7 vì lúc này \(i_{\max }\)
\( \Rightarrow {W_{L\max }} = {1 \over 2}Li_{\max }^2.\)
Chọn đáp án D.
Bài 2: Dao động điện từ trong mạch dao động dao động LC là quá trình
A. Biến đổi không tuần hoàn của điện tích trên tụ điện.
B. Biến đổi theo hàm mũ của cường độ dòng điện.
Advertisements (Quảng cáo)
C. Chuyển hoá tuần hoàn giữa năng lượng từ trường và năng lượng điện trường.
D. Bảo toàn hiệu điện thế giữa hai cực tụ điện.
Giải
Dao động điện từ trong mạch dao động LC là quá trình chuyển hoá tuần hoàn giữa năng lượng từ trường và năng lượng điện trường.
Chọn đáp án C.
Bài 3 trang 123 SGK Vật Lý 12 Nâng cao
Trong một mạch dao động LC, tụ điện có điện dung là \(5\mu F\), cường độ tức thời của dòng điện là\(i = 0,05\sin 2000t(A).\)Tìm độ tự cảm và biểu thức cho điện tích của tụ.
Advertisements (Quảng cáo)
Mạch dao động có \(C = 5(\mu F)\)
Dòng điện có biểu thức \(i = 0,05\sin 2000t\)
Với \(I_0= 0,05\) (A) và \(\omega = 2000(rad/s) \Rightarrow {q_0} = {{{I_0}} \over \omega } = {{0,05} \over {2000}} = 2,{5.10^{ – 5}}(C)\)
Ta có \(\omega = {1 \over {\sqrt {LC} }} \Rightarrow {\omega ^2} = {1 \over {LC}} \Rightarrow L = {1 \over {{\omega ^2}C}} = {1 \over {{{(2000)}^2}{{.5.10}^{ – 6}}}} \)
\(\Rightarrow L = 0,05(H).\)
Điện tích của tụ có biểu thức : (Vì q chậm pha so với \(i\) một góc \({\pi \over 2}\))
\(q = {q_0}\sin (2000t – {\pi \over 2})\)
\(\Rightarrow q = 2,{5.10^{ – 5}}\sin (2000t – {\pi \over 2})\) (C).
Bài 4: Một mạch dao động LC có năng lượng là \({36.10^{ – 6}}J\) và điện dung của tụ điện C là \(2,5\mu F.\)Tìm năng lượng tập trung tại cuộn cảm khi hiệu điện thế giữa hai bản cực của tụ điện là \(3\) V.
Giải
Mạch dao động có năng lượng điện từ \(W = {36.10^{ – 6}}J\)
Tụ điện \(C = 2,5(\mu F)\) có hiệu điện thế giữa hai cực của bản tụ là \(U = 3\) (V)
Năng lượng điện trường tập trung tại tụ điện là:
\({W_C} = {{C{U^2}} \over 2} = {{2,{{5.10}^{ – 6}}{{.3}^2}} \over 2}\)
\(= 1,{125.10^{ – 5}}(J) = 11,{25.10^{ – 6}}(J)\)
Năng lượng từ trường tập trung tại cuộn cảm là:
\( {W_L} = W – {W_C} = {36.10^{ – 6}} – 11,{25.10^{ – 6}} \)
\(= 24,{75.10^{ – 6}}(J).\)

