Câu 14. Giải các phương trình sau :
a. \(\sin 4x = \sin {\pi \over 5}\)
b. \(\sin \left( {{{x + \pi } \over 5}} \right) = – {1 \over 2}\)
c. \(\cos {x \over 2} = \cos \sqrt 2 \)
d. \(\cos \left( {x + {\pi \over {18}}} \right) = {2 \over 5}.\)
a. Ta có:
\(\sin 4x = \sin {\pi \over 5} \Leftrightarrow \left[ {\matrix{{4x = {\pi \over 5} + k2\pi } \cr {4x = \pi – {\pi \over 5} + k2\pi } \cr} \,\,\left( {k \in\mathbb Z} \right) \Leftrightarrow \left[ {\matrix{{x = {\pi \over {20}} + k{\pi \over 2}} \cr {x = {\pi \over 5} + k{\pi \over 2}} \cr} } \right.} \right.\,\,\left( {k \in\mathbb Z} \right)\)
b. Vì \( – {1 \over 2} =- \sin {\pi \over 6} = \sin \left( { – {\pi \over 6}} \right)\) nên :\(\sin \left( {{{x + \pi } \over 5}} \right) = – {1 \over 2} \Leftrightarrow \left[ {\matrix{{{{x + \pi } \over 5} = – {\pi \over 6} + k2\pi } \cr {{{x + \pi } \over 5} = \pi + {\pi \over 6} + k2\pi } \cr} } \right. \Leftrightarrow \left[ {\matrix{{x = – {{11\pi } \over 6} + k10\pi } \cr {x = {{29\pi } \over 6} + k10\pi } \cr} } \right.\,\,\left( {k \in\mathbb Z} \right)\)
c.
\(\cos {x \over 2} = \cos \sqrt 2 \Leftrightarrow {x \over 2} = \pm \sqrt 2 + k2\pi \Leftrightarrow x = \pm 2\sqrt 2 + k4\pi \,\left( {k \in\mathbb Z} \right)\)
d. Vì \(0 < {2 \over 5} < 1\) nên có số \(α\) sao cho \(\cos \alpha = {2 \over 5}.\) Do đó :
\(\cos \left( {x + {\pi \over {18}}} \right) = {2 \over 5} \Leftrightarrow \cos \left( {x + {\pi \over {18}}} \right) = \cos \alpha \Leftrightarrow x = \pm \alpha – {\pi \over {18}} + k2\pi ,k \in \mathbb Z\)
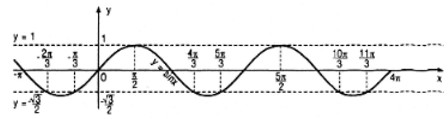
Câu 15. a. Vẽ đồ thị của hàm số \(y = \sin x\) rồi chỉ ra trên đồ thị đó các điểm có hoành độ thuộc khoảng \((-π ; 4π)\) là nghiệm của mỗi phương trình sau :
1. \(\sin x = – {{\sqrt 3 } \over 2}\)
2. \(\sin x = 1\)
b. Cũng câu hỏi tương tự cho hàm số \(y = \cos x\) đối với mỗi phương trình sau
1. \(\cos x = {1 \over 2}\)
2. \(\cos x = -1\).
a. \(1/\,\,\sin x = – {{\sqrt 3 } \over 2} \Leftrightarrow \sin x = \sin \left( { – {\pi \over 3}} \right) \Leftrightarrow \left[ {\matrix{{x = – {\pi \over 3} + k2\pi } \cr {x = {{4\pi } \over 3} + k2\pi } \cr} } \right.\)
*Với \(x = – {\pi \over 3} + k2\pi \,\text{ và }\,x \in \left( { – \pi ;4\pi } \right)\) ta có nghiệm :
\({x_1} = – {\pi \over 3};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_2} = {{5\pi } \over 3};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_3} = {{11\pi } \over 3}\)
* Với \(x = {{4\pi } \over 3} + k2\pi \,\text{ và }\,x \in \left( { – \pi ;4\pi } \right)\) ta có nghiệm :
\({x_4} = – {{2\pi } \over 3};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_5} = {{4\pi } \over 3};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_6} = {{10\pi } \over 3}\)
2/ \(\sin x = 1 \Leftrightarrow x = {\pi \over 2} + k2\pi \)
* Với \(x = {\pi \over 2} + k2\pi \,va\,x \in \left( { – \pi ;4\pi } \right)\) ta có nghiệm :
\({x_1} = {\pi \over 2};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{x_2} = {{5\pi } \over 2}.\)
Xem hình vẽ
b. Tương tự câu a) ta có hình vẽ sau :
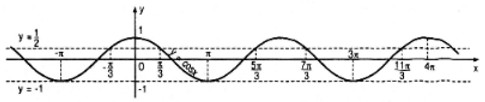
1. Nghiệm của phương trình \(\cos x = {1 \over 2}\) thuộc khoảng \((-π;4π)\) là :
\({x_1} = – {\pi \over 3};\,\,\,\,\,\,\,\,\,\,{x_2} = {\pi \over 3};\,\,\,\,\,\,\,\,\,\,\,{x_3} = {{5\pi } \over 3};\,\,\,\,\,\,\,\,\,\,\,{x_4} = {{7\pi } \over 3};\,\,\,\,\,\,\,\,\,\,\,\,{x_5} = {{11\pi } \over 3}\)
2. Nghiệm của phương trình \(\cos x = -1\) thuộc khoảng \((-π ; 4π)\) là :
\(x_1= -π\) \(x_2 = π\) \(x_3= 3π\)
Câu 16. Tìm nghiệm của các phương trình sau trong khoảng đã cho
a. \(\sin 2x = – {1 \over 2}\,\text{ với }\,0 < x < \pi \)
b. \(\cos \left( {x – 5} \right) = {{\sqrt 3 } \over 2}\,\text{ với }\, – \pi < x < \pi \)
a. Ta có: \(\sin 2x = – {1 \over 2} \Leftrightarrow \sin 2x = \sin \left( { – {\pi \over 6}} \right)\)
\( \Leftrightarrow \left[ {\matrix{{2x = – {\pi \over 6} + k2\pi } \cr {2x = {{7\pi } \over 6} + k2\pi } \cr} } \right. \Leftrightarrow \left[ {\matrix{{x = – {\pi \over {12}} + k\pi } \cr {x = {{7\pi } \over {12}} + k\pi } \cr} } \right.\,\,\left( {k \in \mathbb Z} \right)\)
Với điều kiện \(0 < x < π\) ta có :
* \(0 < – {\pi \over {12}} + k\pi < \pi \Leftrightarrow {1 \over {12}} < k < {{13} \over {12}}\,,\,k \in\mathbb Z\)
Nên\( k = 1\), khi đó ta có nghiệm \(x = {{11\pi } \over {12}}\)
* \(0 < {{7\pi } \over {12}} + k\pi < \pi \Leftrightarrow – {7 \over {12}} < k < {5 \over {12}}\,,\,k \in\mathbb Z\)
Nên \(k = 0\), khi đó ta có nghiệm \(x = {{7\pi } \over {12}}\)
Vậy phương trình đã cho có hai nghiệm trong khoảng \((0 ; π)\) là :
\(x = {{7\pi } \over {12}}\,\text{ và }\,x = {{11\pi } \over {12}}\)
b. \(\cos \left( {x – 5} \right) = {{\sqrt 3 } \over 2} \Leftrightarrow \left[ {\matrix{{x – 5 = {\pi \over 6} + k2\pi } \cr {x – 6 = – {\pi \over 6} + 5 + k2\pi } \cr} } \right. \Leftrightarrow \left[ {\matrix{{x = {\pi \over 6} + 5 + k2\pi } \cr {x = – {\pi \over 6} + 5 + k2\pi } \cr} } \right.\)
Ta tìm \(k\) để điều kiện \(–π < x < π\) được thỏa mãn.
Xét họ nghiệm thứ nhất :
\(\eqalign{
& – \pi < {\pi \over 6} + 5 + k2\pi \Leftrightarrow – 7\pi – 30 < 12k\pi < 5\pi – 30 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow – {7 \over {12}} – {{30} \over {12\pi }} < k < {5 \over {12}} – {{30} \over {12\pi }} \cr
& Vi\, – 1,38 < – {7 \over {12}} – {{30} \over {12\pi }} < k < {5 \over {12}} – {{30} \over {12\pi }} < – 0,37\,,\,k \in\mathbb Z\,\text{ nên }\, \cr
& \,\,\,\,\, – 1,38 < k < – 0,37 \cr} \)
Chỉ có một giá trị \(k\) nguyên thỏa mãn các điều kiện đó là \(k = -1\).
Ta có nghiệm thứ nhất của phương trình là \(x = {\pi \over 6} + 5 – 2\pi = 5 – {{11\pi } \over 6}\)
Tương tự, xét họ nghiệm thứ hai :
\( – \pi < – {\pi \over 6} + 5 + k2\pi < \pi \Leftrightarrow – 5\pi – 30 < 12k\pi < 7\pi – 30.\) Vậy \(k = -1\)
Ta có nghiệm thứ hai của phương trình là \(x = – {\pi \over 6} + 5 – 2\pi = 5 – {{13\pi } \over 6}\)
Vậy : \(x = 5 – {{11\pi } \over 6}\,\text{ và }\,x = 5 – {{13\pi } \over 6}\)
Câu 17. Số giờ có ánh sáng mặt trời của một thành phố A ở vĩ độ 40˚ bắc trong ngày thứ t của một năm không nhuận được cho bởi hàm số
\(d\left( t \right) = 3\sin \left[ {{\pi \over {182}}\left( {t – 80} \right)} \right] + 12\,voi\,t \in \,va\,0 < t \le 365.\)
a. Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày nào trong năm ?
b. Vào ngày nào trong năm thì thành phố A có ít giờ có ánh sáng mặt trời nhất ?
c. Vào ngày nào trong năm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất ?
a. Ta giải phương trình \(d(t) = 12\) với \(t \in\mathbb Z\) và \(0 < t ≤ 365\)
Ta có \(d(t) = 12 \Leftrightarrow \sin \left[ {{\pi \over {182}}\left( {t – 80} \right)} \right] = 0 \Leftrightarrow {\pi \over {182}}\left( {t – 80} \right) = k\pi \)
Advertisements (Quảng cáo)
\( \Leftrightarrow t = 182k + 80\,\left( {\,k \in\mathbb Z} \right)\)
Ta lại có
\(0 < 182k + 80 \le 365 \Leftrightarrow – {{80} \over {182}} < k \le {{285} \over {182}} \Leftrightarrow \left[ {\matrix{{k = 0} \cr {k = 1} \cr} } \right.\)
Vậy thành phố \(A\) có đúng \(12\) giờ ánh sáng mặt trời vào ngày thứ \(80\) (ứng với \(k = 0\)) và ngày thứ \(262\) (ứng với \(k = 1\)) trong năm.
b. Do \(\sin x ≥ -1\) với mọi \(x\) nên thành phố \(A\) có ít giờ ánh sáng mặt trời nhất khi và chỉ khi :
\(\sin \left[ {{\pi \over {182}}\left( {t – 80} \right)} \right] = – 1\,\text{ với }\,t \in \mathbb Z\,\text { và }\,0 < t \le 365\)
Phương trình đó cho ta
\({\pi \over {182}}\left( {t – 80} \right) = – {\pi \over 2} + k2\pi \)
\( \Leftrightarrow t = 364k – 11\,\left( {\,k \in\mathbb Z} \right)\)
Mặt khác,\(0 < 364k – 11 \le 365 \Leftrightarrow {{11} \over {364}} < k \le {{376} \over {364}} \Leftrightarrow k = 1\) (do \(k\) nguyên)
Vậy thành phố \(A\) có ít giờ ánh sáng mặt trời nhất (\(9\) giờ) khi \(t = 353\), tức là vào ngày thứ \(353\) trong năm.
c. Tương tự, ta phải giải phương trình :
\(\eqalign{
& \sin \left[ {{\pi \over {182}}\left( {t – 80} \right)} \right] = 1\,\text{ với }\,t \in\mathbb Z\,\text{ và }\,0 < t \le 365 \cr
& \Leftrightarrow {\pi \over {182}}\left( {t – 80} \right) = {\pi \over 2} + k2\pi \Leftrightarrow t = 364k + 171 \cr
& 0 < 364k + 171 \le 365 \Leftrightarrow – {{171} \over {364}} < k \le {{194} \over {364}} \Leftrightarrow k = 0 \cr} \)
Vậy thành phố \(A\) có nhiều giờ có ánh sáng mặt trời nhất (\(15\) giờ) vào ngày thứ \(171\) trong năm.
Câu 18. Giải các phương trình sau :
a. \(\tan 3x = \tan {{3\pi } \over 5}\)
b. \(\tan(x – 15^0) = 5\)
c. \(\tan \left( {2x – 1} \right) = \sqrt 3 \)
d. \(\cot 2x = \cot \left( { – {1 \over 3}} \right)\)
e. \(\cot \left( {{x \over 4} + 20^\circ } \right) = – \sqrt 3 \)
f. \(\cot 3x = \tan {{2\pi } \over 5}\)
a. \(\tan 3x = \tan {{3\pi } \over 5} \Leftrightarrow 3x = {{3\pi } \over 5} + k\pi \Leftrightarrow x = {\pi \over 5} + k{\pi \over 3}\)
b. \(\tan(x – 15^0) = 5⇔ x = α + 15^0+ k180^0\),
trong đó \(\tan α = 5\) (chẳng hạn, có thể chọn \(α ≈ 78^041’24”\) nhờ dùng máy tính bỏ túi)
c.
\(\eqalign{
& \tan \left( {2x – 1} \right) = \sqrt 3 \Leftrightarrow \tan \left( {2x – 1} \right) = \tan {\pi \over 3} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow 2x – 1 = {\pi \over 3} + k\pi \Leftrightarrow x = {\pi \over 6} + {1 \over 2} + k{\pi \over 2};k \in\mathbb Z \cr} \)
d.
\(\cot 2x = \cot \left( { – {1 \over 3}} \right) \Leftrightarrow 2x = – {1 \over 3} + k\pi \Leftrightarrow x = – {1 \over 6} + k{\pi \over 2}\)
e.
\(\eqalign{
& \cot \left( {{x \over 4} + 20^\circ } \right) = – \sqrt 3 \Leftrightarrow \cot \left( {{x \over 4} + 20^\circ } \right) = \cot \left( { – 30^\circ } \right) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow {x \over 4} + 20^\circ = – 30^\circ + k180^\circ \Leftrightarrow x = – 200^\circ + k720^\circ \cr} \)
f.
\(\cot 3x = \tan {{2\pi } \over 5} \Leftrightarrow \cot 3x = \cot \left( {{\pi \over 2} – {{2\pi } \over 5}} \right) \Leftrightarrow 3x = {\pi \over {10}} + k\pi \Leftrightarrow x = {\pi \over {30}} + k.{\pi \over 3}\)
Câu 19. a.Vẽ đồ thị của hàm số \(y = \tan x\) rồi chỉ ra trên đồ thị đó có các điểm có hoành độ thuộc khoảng \((-π ; π)\) là nghiệm của mỗi phương trình sau
1. \(\tan x = -1\)
2. \(\tan x = 0\)
b. Cũng câu hỏi tương tự cho hàm số \(y = \cot x\) và cho mỗi phương trình sau
1. \(\cot x = {{\sqrt 3 } \over 3}\)
2. \(\cot x = 1\)
a.
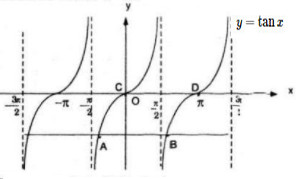
1. Phương trình \(\tan x = -1\) có nghiệm thuộc khoảng \((-π ; π)\) là :
\(x = – {\pi \over 4}\,\text{ và }\,x = {{3\pi } \over 4}\)
Advertisements (Quảng cáo)
2. Phương trình \(\tan x = 0\) có nghiệm thuộc khoảng \((-π ; π)\) là \(x = 0\)
b.
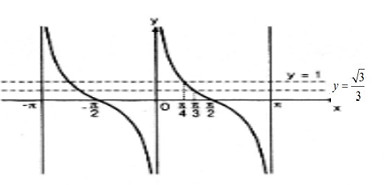
1. Phương trình có nghiệm thuộc khoảng \((-π ; π)\) là :
\(x = {\pi \over 3}\,\text{ và }\,x = – {{2\pi } \over 3}\)
2. Phương trình \(\cot x = 1\) có nghiệm thuộc khoảng \((-π ; π)\) là :
\(x = {\pi \over 4}\,\text{ và }\,x = – {{3\pi } \over 4}\)
Câu 20. Tìm nghiệm của các phương trình sau trên khoảng đã cho
a. \(\tan \left( {2x-{{15}^0}} \right) = 1\) với \( – {180^0} < {\rm{ }}x{\rm{ }} < {\rm{ }}{90^0}\);
b. \(\cot 3x = – {1 \over {\sqrt 3 }}\,\text{ với }\, – {\pi \over 2} < x < 0.\)
a.\(\tan \left( {2x-{{15}^0}} \right) = 1\)\(\Leftrightarrow {\rm{ }}2x{\rm{ }} = {\rm{ }}{15^0} + {\rm{ }}{45^0} + {\rm{ }}k{180^0} \Leftrightarrow {\rm{ }}x{\rm{ }} = {\rm{ }}{30^0} + {\rm{ }}k{90^0}\)
\( – {180^0} < {\rm{ }}{30^0} + {\rm{ }}k{90^0} < {\rm{ }}{90^0} \Leftrightarrow – 2 < {1 \over 3} + k < 1\)
\(\Leftrightarrow k \in \left\{ { – 2; – 1;0} \right\}\)
Vậy các nghiệm của phương trình là \(x = – {150^0},{\rm{ }}x{\rm{ }} = – {60^0}\) và \(x{\rm{ }} = {\rm{ }}{30^0}\)
b.
\(\eqalign{
& \cos 3x = – {1 \over {\sqrt 3 }} \Leftrightarrow x = – {\pi \over 9} + k{\pi \over 3} \cr
& – {\pi \over 2} < – {\pi \over 9} + k{\pi \over 3} < 0 \Leftrightarrow – {7 \over 6} < k < {1 \over 3} \Leftrightarrow k \in \left\{ { – 1;0} \right\} \cr} \)
Vậy các nghiệm của phương trình là \(x = – {{4\pi } \over 9}\,\text{ và }\,x = – {\pi \over 9}.\)
Câu 21. Khi giải phương trình \(\tan x = – \sqrt 3 \) ; bạn Phương nhận thấy \( – \sqrt 3 = \tan \left( { – {\pi \over 3}} \right)\) và viết
\(\tan x = – \sqrt 3 \Leftrightarrow \tan x = \tan \left( { – {\pi \over 3}} \right) \Leftrightarrow x = – {\pi \over 3} + k\pi .\)
Cũng phương trình đó, bạn Quyên lấy \( – \sqrt 3 = \tan {{2\pi } \over 3}\) nên giải như sau :
\(\tan x = – \sqrt 3 \Leftrightarrow \tan x = \tan {{2\pi } \over 3} \Leftrightarrow x = {{2\pi } \over 3} + k\pi .\)
Theo em, ai giải đúng, ai giải sai ?
Cả hai bạn đều giải đúng. Hai họ nghiệm chỉ khác nhau về hình thức, thực chất chỉ là một.
Thực vậy, họ nghiệm \(x = {{2\pi } \over 3} + k\pi \) có thể viết lại là \(x = {{2\pi } \over 3} – \pi + \left( {k + 1} \right)\pi \) hay \(x = – {\pi \over 3} + \left( {k + 1} \right)\pi \) ; đây chính là kết qủa mà Phương tìm được.
Câu 22. Tính các góc của tam giác \(ABC\), biết \(AB = \sqrt 2 cm\), \(AC =\sqrt 3 cm\) và đường cao \(AH = 1cm\). (Gợi ý : Xét trường hợp \(B, C\) nằm khác phía đối với \(H\) và trường hợp \(B, C\) nằm cùng phía đối với \(H\)).
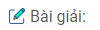
Ta xét hai trường hợp :
a/ \(B\) và \(C\) nằm khác phía đối với \(H\)
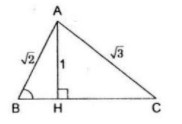
Trong tam giác vuông \(ABH\) ta có :
\(\sin B = {{AH} \over {AB}} = {1 \over {\sqrt 2 }}\)
Suy ra \(\widehat B = 45^\circ \) (chú ý rằng góc \(B\) nhọn)
Trong tam giác \(ACH\) ta có :
\(\sin C = {{AH} \over {AC}} = {1 \over {\sqrt 3 }},\) suy ra \(\widehat C \approx 35^\circ 15’52\)
Từ đó \(\widehat A = 180^\circ – \left( {\widehat B + \widehat C} \right) \approx 99^\circ 44’8\)
b/ \(B\) và \(C\) nằm cùng phía đối với \(H\)
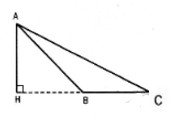
Tương tự như trên ta có :
\(\eqalign{
& \widehat {ABC} = 180^\circ – \widehat {ABH} = 180^\circ – 45^\circ = 135^\circ \cr
& \widehat C \approx 35^\circ 15’52 \cr} \)
Từ đó \(\widehat A = 180^\circ – \left( {\widehat B + \widehat C} \right) \approx 9^\circ 44’8\)
Câu 23. Tìm tập xác định của mỗi hàm số sau :
a. \(y = {{1 – \cos x} \over {2\sin x + \sqrt 2 }}\)
b. \(y = {{\sin \left( {x – 2} \right)} \over {\cos 2x – \cos x}}\)
c. \(y = {{\tan x} \over {1 + \tan x}}\)
d. \(y = {1 \over {\sqrt 3 \cot 2x + 1}}\)
a.\(y = {{1 – \cos x} \over {2\sin x + \sqrt 2 }}\) xác định \( \Leftrightarrow 2\sin x + \sqrt 2 \ne 0\)
\( \Leftrightarrow \sin x \ne – {{\sqrt 2 } \over 2} \Leftrightarrow \left\{ {\matrix{{x \ne – {\pi \over 4} + k2\pi } \cr {x \ne {{5\pi } \over 4} + k2\pi } \cr} } \right.\)
Vậy tập xác định của hàm số đã cho là :
\(D =\mathbb R \backslash \left( {\left\{ { – {\pi \over 4} + k2\pi ,k \in\mathbb Z} \right\} \cup \left\{ {{{5\pi } \over 4} + k2\pi ,k \in\mathbb Z} \right\}} \right)\)
b/ \(y = {{\sin \left( {x – 2} \right)} \over {\cos 2x – \cos x}}\) xác định
\(\eqalign{& \Leftrightarrow \cos 2x \ne \cos x \cr & \Leftrightarrow \left\{ {\matrix{{2x \ne x + k2\pi } \cr {2x \ne – x + k2\pi } \cr} } \right. \Leftrightarrow \left\{ {\matrix{{x \ne k2\pi } \cr {2x \ne k{{2\pi } \over 3}} \cr} } \right. \Leftrightarrow x \ne k{{2\pi } \over 3} \cr} \)
Vậy \(D =\mathbb R \backslash \left\{ {k{{2\pi } \over 3},k \in\mathbb Z} \right\}\)
c/ \(y = {{\tan x} \over {1 + \tan x}}\) xác định \( \Leftrightarrow \tan x \ne – 1 \Leftrightarrow \left\{ {\matrix{{x \ne {\pi \over 2} + k\pi } \cr {x \ne – {\pi \over 4} + k\pi } \cr} } \right.\)
Vậy \(D =\mathbb R \backslash \left( {\left\{ {{\pi \over 2} + k\pi ,k \in\mathbb Z} \right\} \cup \left\{ { – {\pi \over 4} + k\pi ,k \in\mathbb Z} \right\}} \right)\)
d/ \(y = {1 \over {\sqrt 3 \cot 2x + 1}}\) xác định \( \Leftrightarrow \cot 2x \ne – {1 \over {\sqrt 3 }}\)
\( \Leftrightarrow \left\{ {\matrix{{2x \ne k\pi } \cr {2x \ne – {\pi \over 3} + k\pi } \cr} } \right. \Leftrightarrow \left\{ {\matrix{{x \ne k{\pi \over 2}} \cr {x \ne – {\pi \over 6} + k{\pi \over 2}} \cr} } \right.\)
Vậy \(D =\mathbb R \backslash \left( {\left\{ {k{\pi \over 2},k \in\mathbb Z} \right\} \cup \left\{ { – {\pi \over 6} + k{\pi \over 2},k \in\mathbb Z} \right\}} \right)\)
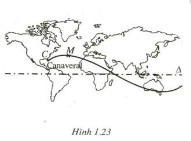
Câu 24. Giả sử một con tàu vũ trụ được phóng lên từ mũi Ca-na-vơ-ran (Canaveral) ở Mĩ. Nó chuyển động theo một quỹ đạo được mô tả trên một bản đồ phẳng (quanh đường xích đạo) của mặt đất
như hình 1.23 : điểm \(M\) mô tả cho con tàu, đường thẳng \(∆\) mô tả cho đường xích đạo.
Khoảng cách \(h\) (kilomet) từ \(M\) đến \(∆\) được
tính theo công thức \(h = |d|\), trong đó
\(d = 4000\cos \left[ {{\pi \over {45}}\left( {t – 10} \right)} \right],\)
Với \(t\) (phút) là thời gian trôi qua kể từ khi con tàu đi vào quỹ đạo, \(d > 0\) nếu \(M\) ở phía trên \(∆\), \(d < 0\) nếu \(M\) ở phía dưới \(∆\).
a. Giả thiết rằng con tàu đi vào quỹ đạo ngay từ khi phóng lên tại mũi Ca-na-vơ-ran (tức là ứng với \(t = 0\)). Hãy tính khoảng cách từ điểm \(C\) đến đường thẳng \(∆\), trong đó \(C\) là điểm trên bản đồ biểu diễn cho mũi Ca-na-vơ-ran.
b. Tìm thời điểm sớm nhất sau khi con tàu đi vào quỹ đạo để có \(d = 2000\).
c. Tìm thời điểm sớm nhất sau khi con tàu đi vào quỹ đạo để có \(d = -1236\).
(Tính chính xác các kết quả đến hàng phần nghìn).
a. Vì \(t = 0\) nên \(d = 4000\cos \left( { – {{10\pi } \over {45}}} \right) = 4000\cos {{2\pi } \over 9}.\) Do đó :
\(h = |d| ≈ 3064,178 (km)\)
b.
\(\eqalign{& d = 2000 \Leftrightarrow 4000\cos \left[ {{\pi \over {45}}\left( {t – 10} \right)} \right] = 2000\Leftrightarrow \cos \left[ {{\pi \over {45}}\left( {t – 10} \right)} \right] = {1 \over 2} \cr & \Leftrightarrow {\pi \over {45}}\left( {t – 10} \right) = \pm {\pi \over 3} + k2\pi \Leftrightarrow t = 10 \pm 15 + 90k \Leftrightarrow \left[ {\matrix{{t = 25 + 90k} \cr {t = – 5 + 90k} \cr} } \right. \cr} \)
Chú ý rằng \(t > 0\) ta thấy ngay giá trị nhỏ nhất của \(t\) là \(t = 25\). Vậy \(d = 2000 (km)\) xảy ra lần đầu tiên sau khi phóng con tàu vào quỹ đạo được \(25\) phút.
c.
\(\eqalign{
& d = – 1236 \Leftrightarrow 4000\cos \left[ {{\pi \over {45}}\left( {t – 10} \right)} \right] = – 1236 \Leftrightarrow \cos \left[ {{\pi \over {45}}\left( {t – 10} \right)} \right] = – 0,309 \cr
& \Leftrightarrow {\pi \over {45}}\left( {t – 10} \right) = \pm \alpha + k2\pi \,\left( {\text{ với }\,k \in \mathbb Z\,\text{ và }\,\cos \alpha = – 0,309} \right) \cr
& \Leftrightarrow t = \pm {{45} \over \pi }\alpha + 10 + 90k \cr} \)
Sử dụng bảng số hoặc máy tính bỏ túi, ta có thể chọn \(α ≈ 1,885\). Khi đó ta có :
\(t ≈ ± 27,000 + 10 + 90k\), tức là \(t ≈ – 17,000 + 90k\) hoặc \(t ≈ 37,000 + 90k\)
Dễ thấy giá trị dương nhỏ nhất của \(t\) là \(37,000\). Vậy \(d = -1236 (km)\) xảy ra lần đầu tiên là \(37,000\) phút sau khi con tàu được phóng vào quỹ đạo.
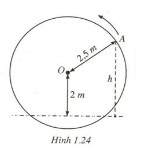
Câu 25. Một chiếc guồng nước có dạng hình tròn bán kính \(2,5m\) ;trục của nó đặt cách mặt nước \(2m\) (h.1.24). Khi guồng quay đều, khoảng cách \(h\) (mét) từ một chiếc gầu gắntại điểm \(A\) của guồng đến mặt nước được tính theo công thức \(h = |y|\), trong đó
\(y = 2 + 2,5\sin \left[ {2\pi \left( {x – {1 \over 4}} \right)} \right]\)
Với \(x\) là thời gian quay guồng (\(x ≥ 0\)), tính bằng phút ; ta quy ước rằng \(y > 0\) khi gầu ở bên trên mặt nước và \(y < 0\) khi gầu ở dưới nước (xem bài đọc thêm về dao động điều hòa trang 15). Hỏi :
a. Khi nào thì chiếc gầu ở vị trí thấp nhất ?
b. Khi nào thì chiếc gầu ở vị trí cao nhất ?
c. Chiếc gầu cách mặt nước \(2m\) lần đầu tiên khi nào ?
a. Chiếc gầu ở vị trí thấp nhất khi \(\sin \left[ {2\pi \left( {x – {1 \over 4}} \right)} \right] = – 1.\) Ta có :
\(\sin \left[ {2\pi \left( {x – {1 \over 4}} \right)} \right] = – 1 \Leftrightarrow 2\pi \left( {x – {1 \over 4}} \right) = – {\pi \over 2} + k2\pi \Leftrightarrow x = k\,\left( {\,k \in\mathbb Z} \right)\)
Điều đó chứng tỏ rằng chiếc gầu ở vị trí thấp nhất tại các thời điểm 0 phút ; 1 phút ; 2 phút ; 3 phút…
b. Chiếc gầu ở vị trí cao nhất khi \(\sin \left[ {2\pi \left( {x – {1 \over 4}} \right)} \right] = 1.\) Ta có :
\(\sin \left[ {2\pi \left( {x – {1 \over 4}} \right)} \right] = 1 \Leftrightarrow 2\pi \left( {x – {1 \over 4}} \right) = {\pi \over 2} + k2\pi \Leftrightarrow x = {1 \over 2} + k\,\left( {\,k \in N} \right)\)
Điều đó chứng tỏ chiếc gàu ở vị trí cao nhất tại các thời điểm 0,5 phút; 1,5 phút ; 2,5 phút ; 3,5 phút …
c. Chiếc gàu cách mặt nước 2 mét khi \(\sin \left[ {2\pi \left( {x – {1 \over 4}} \right)} \right] = 0,\) nghĩa là tại các thời điểm \(x = {1 \over 4} + {1 \over 2}k\) (phút); do đó lần đầu tiên nó cách mặt nước 2 mét khi quay được \({1 \over 4}\) phút (ứng với \(k = 0\)).
Câu 26. Dùng công thức biến đổi tổng thành tích , giải các phương trình sau :
a. \(\cos 3x = \sin 2x\)
b. \(\sin (x – 120˚) – \cos 2x = 0\)
a.
\(\eqalign{& \cos 3x = \sin 2x \Leftrightarrow \cos 3x – \cos \left( {{\pi \over 2} – 2x} \right) = 0 \cr & \Leftrightarrow – 2\sin \left( {{x \over 2} + {\pi \over 4}} \right)\sin \left( {{{5x} \over 2} – {\pi \over 4}} \right) = 0 \cr & \Leftrightarrow \left[ {\matrix{{{x \over 2} + {\pi \over 4} = k\pi } \cr {{{5x} \over 2} – {\pi \over 4} = k\pi } \cr} } \right. \Leftrightarrow \left[ {\matrix{{x = – {\pi \over 2} + k2\pi } \cr {x = {\pi \over {10}} + k{{2\pi } \over 5}} \cr} } \right. \cr} \)
b.
\(\eqalign{& \sin \left( {x – 120^\circ } \right) – \cos 2x = 0 \Leftrightarrow \cos \left( {210^\circ – x} \right) – \cos 2x = 0 \cr & \Leftrightarrow – 2\sin \left( {{x \over 2} + 105^\circ } \right)\sin \left( {105^\circ – {{3x} \over 2}} \right) = 0 \cr & \Leftrightarrow \left[ {\matrix{{{x \over 2} + 105^\circ = k180^\circ } \cr {105^\circ – {{3x} \over 2} = k180^\circ } \cr} } \right. \Leftrightarrow \left[ {\matrix{{x = – 210^\circ + k360^\circ } \cr {x = 70^\circ + k120^\circ } \cr} } \right. \cr} \)

