Bài 1: Cho hai đường thẳng phân biệt \(a,b\) và mặt phẳng \((\alpha)\). Các mệnh đề sau đây đúng hay sai?
a) Nếu \(a//(\alpha)\) và \(b\bot (\alpha)\) thì \(a\bot b\)
b) Nếu \(a//(\alpha)\) và \(b\bot a\) thì \(b\bot (\alpha)\)
c) Nếu \(a//(\alpha)\) và \(b// (\alpha)\) thì \(b//a\)
d) Nếu \(a\bot (\alpha)\) và \(b\bot a\) thì \(b// (\alpha)\)
a) Đúng
b) Sai
c) Sai
d) Sai.
Bài 2: Cho tứ diện \(ABCD\) có hai mặt \(ABC\) và \(BCD\) là hai tam giác cân có chung cạnh đáy \(BC\).Gọi \(I\) là trung điểm của cạnh \(BC\).
a) Chứng minh rằng \(BC\) vuông góc với mặt phẳng \(ADI\).
b) Gọi \(AH\) là đường cao của tam giác \(ADI\), chứng minh rằng \(AH\) vuông góc với mặt phẳng \(BCD\).
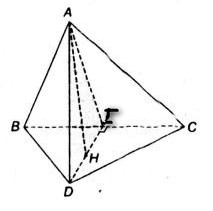
a) Tam giác \(ABC\) cân tại \(A\) nên ta có đường trung tuyến ứng với cạnh đáy đồng thời là đường cao do đó: \(AI\bot BC\)
Tương tự ta có: \(DI\bot BC\)
Advertisements (Quảng cáo)
Ta có:
$$\left. \matrix{
AI \bot BC \hfill \cr
DI \bot BC \hfill \cr
AI \cap DI = {\rm{\{ }}I{\rm{\} }} \hfill \cr} \right\} \Rightarrow BC \bot (ADI)$$
b) Ta có \(AH\) là đường cao của tam giác \(ADI\) nên \(AH\bot DI\)
Mặt khác: \(BC\bot (ADI)\) mà \(AH\subset (ADI)\) nên \(AH\bot BC\)
Ta có
$$\left. \matrix{
AH \bot BC \hfill \cr
AH \bot DI \hfill \cr
BC \cap DI = {\rm{\{ }}I{\rm{\} }} \hfill \cr} \right\} \Rightarrow AH \bot (BCD)$$
Bài 3: Cho hình chóp \(S.ABCD\) có đáy là hình thoi \(ABCD\) và có \(SA=SB=SC=SD\).Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Chứng minh rằng:
a) Đường thẳng \(SO\) vuông góc với mặt phẳng \((ABCD)\);
b) Đường thẳng \( AC\) vuông góc với mặt phẳng \((SBD)\) và đường thẳng \(BD\) vuông góc với mặt phẳng \(SAC\).
Advertisements (Quảng cáo)
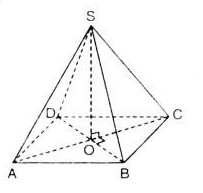
a) Theo giả thiết \(SA=SC\) nên tam giác \(SAC\) cân tại \(S\)
\(O\) là giao của hai đường chéo hình bình hành nên \(O\) là trung điểm của \(AC\) và \(BD\).
Do đó \(SO\) vừa là trung tuyến đồng thời là đường cao trong tam giác \(SAC\) hay \(SO\bot AC\) (1)
Chứng minh tương tự ta được: \(SO\bot BD\) (2)
Từ (1) và (2) suy ra \(SO\bot (ABCD)\).
b) \(ABCD\) là hình thoi nên \(AC\bot BD\) (3)
Từ (1) và (3) suy ra \(AC\bot (SBD)\)
Từ (2) và (3) suy ra \(BD\bot (SAC)\)
Bài 4: Cho tứ diện \(OABC\) có ba cạnh \(OA, OB, OC\) đôi một vuông góc. Gọi \(H\) là chân đường vuông góc hạ từ \(O\) tới mặt phẳng \((ABC)\). Chứng minh rằng:
a) H là trực tâm của tam giác \(ABC\);
b) \(\frac{1}{OH^{2}}=\frac{1}{OA^{2}}+\frac{1}{OB^{2}}+\frac{1}{OC^{2}}.\)
Hướng dẫn.
(h.3.32)
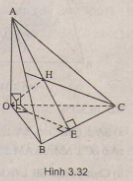
a) \(H\) là hình chiếu của \(O\) trên mp \((ABC)\) nên \(OH ⊥ (ABC) \Rightarrow OH ⊥ BC\). (1)
Mặt khác: \(OA ⊥ OB\), \(OA ⊥ OC\)
\(\Rightarrow OA ⊥ (OBC) \Rightarrow OA ⊥ BC\) (2)
Từ (1) và (2) suy ra \(BC ⊥ (AOH) \Rightarrow BC ⊥ AH\). Chứng minh tương tự ta được \(AB ⊥ CH \)
\(\Rightarrow H\) là trực tâm của tam giác \(ABC\).
b) Trong mặt phẳng \((ABC)\) gọi \(E = AH ∩ BC\), \(OH ⊥ (ABC)\), \(AE ⊂ (ABC) \Rightarrow OH ⊥ AE\) tại \(H\);
\(OA ⊥ (ABC), OE ⊂ (ABC) \Rightarrow OA ⊥ OE\) tức là \(OH\) là đường cao của tam giác vuông \(OAE\).
Mặt khác \(OE\) là đường cao của tam giác vuông \(OBC\)
Do đó: \(\frac{1}{OH^{2}}=\frac{1}{OA^{2}}+\frac{1}{OE^{2}} =\frac{1}{OA^{2}}+\frac{1}{OB^{2}}+\frac{1}{OC^{2}}.\)
Nhận xét: Biểu thức này là mở rộng của công thức tính đường cao thuộc cạnh huyền của tam giác vuông: \(\frac{1}{h^{2}}=\frac{1}{b^{2}}+\frac{1}{c^{2}} .\)

