Bài 37 Các hiện tượng bề mặt của chất lỏng SBT Lý lớp 10. Giải bài 37.8, 37.9, 37.10 trang 88, 89 Sách bài tập Vật lí 10. Câu 37.8: Một bình có ống nhỏ giọt ở đầu phía dưới…
Bài 37.8: Một bình có ống nhỏ giọt ở đầu phía dưới. Rượu chứa trong bình chảy khỏi ống nhỏ giọt này thành từng giọt cách nhau 2,0 s. Miệng ống nhỏ giọt có đường kính 2,0 mm. Sau khoảng thời gian 720 s, khối lượng rượu chảy khỏi ống là 10 g. Xác định hệ số căng bề mặt của rượu. Coi rằng chỗ thắt của giọt rượu khi nó bắt đầu rơi khỏi miệng ống nhỏ giọt có đường kính bằng đường kính của ống nhỏ giọt. Lấy g = 9,8 m/s2.
Trọng lượng P của mỗi giọt rượu khi bắt đầu rơi khỏi miệng ống nhỏ giọt có độ lớn bằng lực căng bề mặt Fc của rượu tác dụng lên chu vi của miệng ống nhỏ giọt, tức là :
P = Fc = σl = σπd
với σ là hệ số căng bề mặt của rượu và l = πd là chu vi của miệng ống nhỏ giọt.
Gọi M là khối lượng rượu chảy khỏi miệng ống trong thời gian t. Vì hai giọt rượu kế tiếp chảy khỏi miệng ống cách nhau 2,0 s nên trọng lượng P mỗi giọt tính bằng :
\(P = {{Mg} \over {{t \over 2}}} = {{2Mg} \over t}\)
Từ đó ta tìm được : \(\sigma = {{2Mg} \over {\pi dt}} = {{{{2.10.10}^{ – 3}}.9,8} \over {3,{{14.2.10}^{ – 3}}.720}} \approx 4,{3.10^{ – 2}}\left( {N/m} \right)\)
Bài 37.9 : Một vòng nhôm đặt nằm ngang tiếp xúc với mặt nước. Vòng nhôm có đường kính trong 50 mm, đường kính ngoài 52 mm và cao 50 mm. Cho biết khối lượng riêng của nhôm là 2800 kg/m3, hệ số căng bề mặt của nước là 73.10-3 N. Lấy g = 9,8 m/s2. Xác định lực kéo để có thể bứt vòng nhôm lên khỏi mặt nước.
Advertisements (Quảng cáo)
Lực kéo để bứt vòng nhôm ra khỏi mặt nước có độ lớn bằng :
F = P + Fc
trong đó P = mg là trọng lượng cùa vòng nhôm được tính theo công thức :
\(P = mg = DVg = D{\pi \over 4}\left( {d_2^2 – d_1^2} \right)hg\)
với D là khối lượng riêng và \(V = {\pi \over 4}\left( {d_2^2 – d_1^2} \right)h\) là thể tích của vòng nhôm.
Lực căng bể mặt Fc của nước tác dụng lên hai mặt (trong và ngoài) của vòng nhôm tính theo công thức:
Advertisements (Quảng cáo)
Fc = σπd1 + σπd2 = σπ(d1 + d2)
Thay số, ta tìm được :
\(P = 2800.{{3,14} \over 4}\left[ {{{\left( {{{52.10}^{ – 3}}} \right)}^2} – {{\left( {{{50.10}^{ – 3}}} \right)}^2}} \right]{.50.10^{ – 3}}.9,8 \approx 21,{9.10^{ – 2}}N\)
\({F_c} = {73.10^{ – 3}}.3,14.\left( {{{50.10}^{ – 3}} + {{52.10}^{ – 3}}} \right) \approx 2,{3.10^{ – 2}}\)
Như vậy lực kéo để có thể bứt vòng nhôm lên khỏi mặt nước bằng :
F ≈ 21,9.10-2 +2.3.10-2 = 24,2.10-2 N
Bài 37.10*: Một ống mao dẫn dài và mỏng có hai đầu đều hở được cắm thẳng đứng xuống nưởc sao cho toàn bộ chiều dài của ống ngập trong nước. Dùng tay bịt kín đầu dưới của ống và nhấc ống thẳng đứng lên khỏi nước. Sau đó buông nhẹ tay để đầu dưới của ống lại hở. Xác định độ cao của cột nước còn đọng trong ống. Cho biết đường kính của ống là 2,0 mm, khối lượng riêng của nước là 1000 kg/m3 và hệ số căng bể mặt của nước là 72,5.10-3 N/m, lấy g ≈ 9,8 m/s2.

Cột nước còn đọng lại được trong ống mao dẫn là do tác dụng cân bằng giữa trọng lượng P của cột nước với tổng các lực dính ướt Fd của thành ống tạo thành mặt khum lõm ở đầu trên và mặt khum lồi ở đầu dưới của cột nước (H.37.3G). Tại vị trí tiếp xúc giữa hai mặt khum của cột nước với thành ống, các lực dính ướt Fd đều hướng thẳng đứng lên phía trên và có cùng độ lớn với lực căng bề mặt Fc của nước.
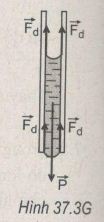
Fd = Fc = σπd
với d là đường kính của ống mao dẫn và σ là hệ số căng bề mặt của nước. Nếu gọi D là khối lượng riêng của nước và h là độ cao của cột nước trong ống thì trọng lượng cột nước bằng : \(P = mg = Dgh{{\pi {d^2}} \over 4}\)
Khi đó điều kiện cân bằng của cột nước đọng lại trong ống là :
\(P = 2{F_d} = > Dgh{{\pi {d^2}} \over 4} = 2\sigma \pi d\)
Từ đó suy ra : \(h = {{8\sigma } \over {Dgd}} = {{{{8.72.10}^{ – 3}}} \over {1000.9,8.2,{{0.10}^{ – 3}}}} \approx 29,4\left( {mm} \right)\).

