Bài 37.5: Một mẩu gỗ hình lập phương có khối lượng 20 g được đặt nổi trên mặt nước. Mẩu gỗ có cạnh dài 30 mm và dính ướt nước hoàn toàn. Cho biết nước có khối lượng riêng là 1000 kg/m3 và hệ số căng bề mặt là 0,072 N/ Lấy g = 9,8 m/s2. Xác định độ ngập sâu trong nước của mẩu gỗ.
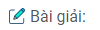
Do mẩu gỗ bị nước dính ướt hoàn toàn, nên lực căng bề mặt Fc tác dụng lên mẩu gỗ hướng thẳng đứng xuống dưới. Điều kiện để mẩu gỗ nổi trên mặt nước là tổng của trọng lực Pp và lực căng bề mặt Fc phải cân bằng với lực đẩy Ác-si-mét FA (H.37.1G):
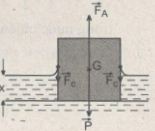
P + Fc = FA
Gọi a là độ dài mỗi cạnh của mẩu gỗ, x là độ ngập sâu trong nước của mẩu gỗ, D và σ là khối lượng riêng và hệ số căng bề mặt của nước. Thay P = mg, Fc = σ4a và FA = Da2xg (bằng trọng lượng nước bị phần mẩu gỗ chìm trong nước chiếm chỗ), ta tìm được:
\(mg + \sigma 4a = D{a^2}xg = > x = {{mg + \sigma 4a} \over {D{a^2}g}}\)
Thay số: \(x = {{{{20.10}^{ – 3}}.9,8 + 0,{{072.4.30.10}^{ – 3}}} \over {1000.{{\left( {{{30.10}^{ – 3}}} \right)}^2}.9,8}} \approx \left( {2,2 + 0,1} \right)cm = 2,3cm\)
Như vậy lực dính ướt có tác dụng làm mẩu gỗ chìm sâu thêm 0,1 cm chiếm tỉ lệ khoảng hơn 4% độ ngập sâu của mẩu gỗ.
Bài 37.6: Một chiếc kim hình trụ bằng thép có bôi một lớp mỏng dầu nhờn ở mặt ngoài được đặt nằm ngang và nổi trên mặt nước. Hãy xác định đường kính lớn nhất của chiếc kim sao cho độ chìm sâu trong nước của chiếc kim bằng bán kính của nó. Đường kính chiếc kim bằng 5% độ dài của nó. Cho biết khối lượng riêng của thép là 7800 kg/m3 và của nước là 1000 kg/m3 hệ số căng bề mặt của nước là 0,072 N/m, lấy g ≈ 9,8 m/s2.
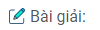
Advertisements (Quảng cáo)
Muốn chiếc kim nổi trên mặt nước thì hiệu số giữa trọng lượng P và lực đẩy Ác-si-mét FA tác dụng lên chiếc kim phải lớn hơn hoặc bằng lực căng bề mặt Fc của phần mặt nước đỡ chiếc kim nổi trên nó (H.37.2G) :
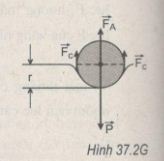
P – FA > Fc
Gọi d là bán kính, l là chiều dài và D là khối lượng riêng của chiếc kim, còn D0 và σ là khối lượng riêng và hệ số căng bề mặt của nước.
Thay \(P = mg = D{{\pi {d^2}} \over 4}\lg ,{F_c} = \sigma 2\left( {d + l} \right)\)
và \({F_A} = {D_0}{1 \over 2}{{\pi {d^2}} \over 4}\lg \) (trọng lượng nước bị một nửa phần chiếc kim chìm
Advertisements (Quảng cáo)
trong nước chiếm chỗ), đổng thời chú ý rằng d = 0,05l hay l = 20d, ta tìm được :
\(D{{\pi {d^2}} \over 4}20dg – {D_0}{{\pi {d^2}} \over 8}20dg \ge \sigma 2\left( {d + 20d} \right)\)
Từ đó suy ra : \(d \ge \sqrt {{{16,8\sigma } \over {\pi g\left( {2D – {D_0}} \right)}}} \)
Thay số, ta được : \({d_{\max }} = \sqrt {{{16,8.0,072} \over {3,14.9,8.\left( {2.7800 – 1000} \right)}}} \approx 1,64mm\)
Bài 37.7: Một lượng nước trong ống nhỏ giọt ở 200C chảy qua miệng ống tạo thành 48 giọt. Cùng lượng nước này ờ 40°C chảy qua miệng ống tạo thành 50 giọt. Cho biết hệ số căng bề mặt của nước ở 20°C là 72,5. 10-3 N/m. Bỏ qua sự dãn nở nhiệt của nước. Xác định hệ số căng bề mặt của nước ở 40°C, lấy g ≈ 9,8 m/s2.
Khi giọt nước rơi khỏi miệng ống nhỏ giọt thì trọng lượng P của nó bằng lực căng bề mặt Fc tác dụng lên giọt nước tại miệng ống :
P = Fc
Thay \(P = {{mg} \over n} = {{DVg} \over n}\) và Fc = σπd, với m và V là khối lượng và thể tích của khối nước trong ống nhỏ giọt, n là số giọt nước chảy ra khỏi miệng ống, d là đường kính miệng dưới của ống, D và σ là khối lượng riêng và hệ số căng bề mặt của nước, ta tìm được :
\(\sigma = {{{F_c}} \over {\pi d}} = {{DVg} \over {n\pi d}}\)
Với cùng thể tích V của nước trong ống, thì hệ số căng bề mặt của nước :
– Ở 20°C có số giọt nước n1 chảy khỏi miệng ống sẽ là : \({\sigma _1} = {{DVg} \over {{n_1}\pi d}}\)
– Ở 40°C có số giọt nước n2 chảy ra khỏi miệng ống sẽ là :\({\sigma _2} = {{DVg} \over {{n_2}\pi d}}\)
Từ đó suy ra : \({{{\sigma _2}} \over {{\sigma _1}}} = {{{n_1}} \over {{n_2}}} = > {\sigma _2} = {\sigma _1}{{{n_1}} \over {{n_2}}}\)
Thay số, ta tìm được : \({\sigma _2} = 72,{5.10^{ – 3}}.{{48} \over {50}} = 69,{6.10^{ – 3}}\left( {N/m} \right)\)

