Câu C1: Hãy nhắc lại sự mô tả cấu trúc trật tự gần ( xem mục 4. Bài 50)
Xét trong một phạm vi hẹp ( trong một khoảng thời gian ) thì các hạt cũng được sắp xếp theo một trật tự nào đó. Nhưng xét trong một phạm vi lớn hơm thì trật tự đó không còn giữa được nữa – sắp xếp như thế gọi là sắp xếp theo “trật tự gần”
Câu C2: Hãy cho biết hình dạng bề ngoài của vỏ bong bóng xà phòng
Vỏ bong bóng xà phòng là một khối chất lỏng (hình cầu) có hai mặt ngoài đó là bề mặt cầu bên ngoài và bề mặt cầu bên trong
Bài 1: một cọng rơm dài 8,0 cm nổi trên mặt nước. Người ta nhỏ dung dịch xà phòng xuống bề mặt của cọng rơm và giả sử nước xà phòng chỉ lan ra một bên mà thôi. Hỏi cọng rơm chuyển động về phía nào ? vì sao?
Lực tác dụng vào cọng rơm là bao nhiêu ?
Hệ số căng bề mặt của nước ( ở \({20^0}C\)) là \({\sigma _1} = 72,{8.10^{ – 3}}N/m\)
Advertisements (Quảng cáo)
Hệ số căng của dung dịch xà phòng \({\sigma _2} = 40,{0.10^{ – 3}}N/m\)
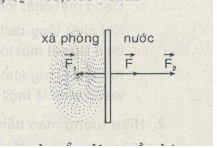
Khi thả nổi cọng rơm trên mặt nước rồi nhỏ dung dịch xà phòng vào một bên thì cọng rơm chịu tác dụng của hai lực căng bề mặt cùng phương, ngược chiều nhau có độ lớn : \({\sigma _1}l = {F_1} < {F_2} = {\sigma _2}l\)
Nên hợp lực \(\overrightarrow F \) hướng theo \(\overrightarrow {{F_2}} \Leftrightarrow \) cọng rơm chuyển động về phía nước.
Advertisements (Quảng cáo)
Độ lớn của lực:
\(\eqalign{
& F = {F_2} – {F_1} = ({\sigma _2} – {\sigma _1})l \cr
& = (72,8 – 40,0){.10^{ – 3}}{.8.10^{ – 2}} = 2,{6.10^{ – 3}}(N) \cr} \)
Bài 2: Để xác định hệ số căng bề mặt của nước , người ta dùng một ống nhỏ giọt mà đầu dưới của ống có đường kính trong 2 mm. Khối lượng của 40 giọt nước ngỏ xuống là 1,9 g. hãy tính hệ số căng bề mặt của nước nếu coi trọng lượng của mỗi giọt nước rơi xuống vừa đúng bằng lực căng bề mặt đặt lên vòng tròn trong ở đầu dưới của ống nhỏ giọt.
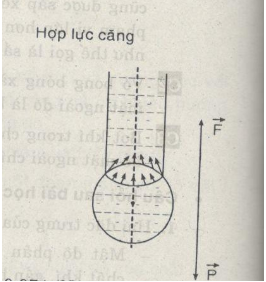
Khối lượng của \(n=40\) giọt là \(m=1,9(g)\)
Trọng lượng của một giọt nước khi rơi :
\(P = m_1g = {{mg} \over n}\)
Chiều dài đường giới hạn: \(l = \pi d\)
Độ lớn của lực căng bề mặt: \(F = \sigma l = \sigma \pi d\)
Điều kiện cân bằng lực tác dụng lên giọt nước ngay trước khi rơi là:
\(\eqalign{
& F = P \Leftrightarrow \sigma \pi d = {{mg} \over n} \cr
& \Rightarrow \sigma = {{mg} \over {n\pi d}} = {{1,{{9.10}^{ – 3}}.9,8} \over {40.3,{{14.2.10}^{ – 3}}}} = 0,074(N/m) \cr} \)

