Câu 7. Qua phép đối xứng trục \({D_a}\) (a là trục đối xứng), đường thẳng \(d\) biến thành đường thẳng \(d’\). Hãy trả lời các câu hỏi sau:
a. Khi nào thì \(d\) song song với \(d’\)?
b. Khi nào thì \(d\) trùng với \(d’\) ?
c. Khi nào thì \(d\) cắt \(d’\)? Giao điểm của \(d\) và \(d’\)có tính chất gì ?
d. Khi nào \(d\) vuông góc với \(d’\)?
Giải :
a. Khi d // a thì d // d’
b. Khi d vuông góc với a hoặc d trùng với a thì d trùng với d’
c. Khi d cắt a nhưng không vuông góc với a. Khi đó giao điểm của d với d’ nằm trên a
d. Khi góc giữa d và a bằng \(45^0\) thì \(d ⊥ d’\)
Câu 8. Trong mặt phẳng tọa độ Oxy, cho các đường tròn (C1) và (C2) lần lượt có phương trình:
\(\eqalign{
& \left( {{C_1}} \right):{x^2} + {y^2} – 4x + 5y + 1 = 0 \cr
& \left( {{C_2}} \right):{x^2} + {y^2} + 10y – 5 = 0 \cr} \)
Viết phương trình ảnh của mỗi đường tròn trên qua phép đối xứng có trục Oy
Ta có:
\(\eqalign{
& {x^2} + {y^2} – 4x + 5y + 1 = 0 \cr
& \Leftrightarrow {\left( {x – 2} \right)^2} + {\left( {y + {5 \over 2}} \right)^2} = {{37} \over 4} \cr} \)
\((C_1)\) có tâm \({I_1}\left( {2; – {5 \over 2}} \right)\) và bán kính \({R_1} = {{\sqrt {37} } \over 2}\)
Gọi \(I’_1\) là ảnh của \(I_1\) qua phép đối xứng có trục Oy thì \(I{‘_1}\left( { – 2; – {5 \over 2}} \right)\)
Vậy phương trình ảnh \((C’_1)\) của \((C_1)\) qua phép đối xứng trục Oy là:
\(\eqalign{
& {\left( {x + 2} \right)^2} + \left( {y + {5 \over 2}} \right) = {{37} \over 4} \cr
& \Leftrightarrow {x^2} + {y^2} + 4x + 5y + 1 = 0 \cr} \)
Advertisements (Quảng cáo)
Câu 9. Cho góc nhọn xOy và một điểm A nằm trong góc đó. Hãy xác định điểm B trên Ox và điểm C trên Oy sao cho tam giác ABC có chu vi nhỏ nhất
Giải
Xét tam giác bất kì ABC có B và C lần lượt nằm trên hai tia Ox và Oy.
Gọi A’ và A” là các điểm đối xứng với điểm A lần lượt qua các đường thẳng Ox và Oy.
Ta có \(AB = A’B\) và \(AC = A”C\) ( do các \(△ABA’\) và \(△ACA”\) là các tam giác cân).
Gọi \(2p\) là chu vi của tam giác ABC thì: \(2p = AB + BC + CA = A’B + BC + CA” ≥ A’A”\)
Dấu “=” xảy ra khi bốn điểm \(A’, B, C, A”\) thẳng hàng.
Suy ra để chu vi tam giác ABC bé nhất thì phải lấy B và C lần lượt là giao điểm của đoạn thẳng A’A” với hai tia Ox và Oy (các giao điểm đó tồn tại vì góc xOy nhọn)
Câu 10. Cho hai điểm B,C cố định nằm trên đường tròn và điểm A thay đổi trên đường tròn đó. Hãy dùng phép đối xứng trục để chứng minh rằng trực tâm H của tam giác ABC nằm trên một đường tròn cố định
Khi BC không phải là đường kính, gọi là giao điểm của đường thẳng AH với đường tròn . Chứng minh rằng đối xứng với qua đường thẳng BC
Giải
Advertisements (Quảng cáo)
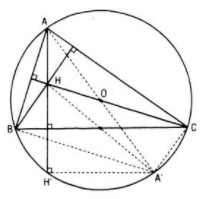
Trường hợp BC là đường kính thì H trùng A, do đó H nằm trên đường tròn cố định (O ; R) Xét trường hợp BC không là đường kính.
Giả sử đường thẳng AH cắt đường tròn (O ; R)
tại H’.Như vậy với mỗi điểm A ∈ (O ; R), khác
với B và C thì ta xác định điểm H’ ∈ (O ; R).
Gọi AA’ là đường kính của đường tròn (O ; R)
thì A’B // CH (vì cùng vuông góc với AB) và
A’C // BH (vì cùng vuông góc với AC) nên
A’BHC là hình bình hành. Vậy BC đi qua
trung điểm của HA’
Mặt khác BC // A’H’ (vì cùng vuông góc với AH) nên BC cũng đi qua trung điểm của HH’, do đó H và H’ đối xứng với nhau qua BC
Nếu gọi Đ là phép đối xứng có trục là đường thẳng BC thì Đ biến H’ thành H. Nhưng H’ luôn luôn nằm trên (O ; R) nên H nằm trên đường tròn cố định là ảnh của đường tròn (O ; R) qua phép đối xứng trục Đ
Cách khác: Gọi H’ là điểm đối xứng của H qua BC. Chứng minh tứ giác ABH’C nội tiếp, từ đó suy ra H’ nằm trên (O ; R)
Câu 11. a. Chỉ ra trục đối xứng (nếu có) của mỗi hình sau đây (mỗi hình là một từ bao gồm một số chữ cái):
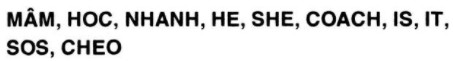
b. Chứng minh rằng đồ thị của hàm số chẵn luôn có trục đối xứng
Giải
a.
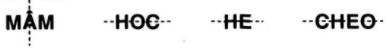
b. Trục Oy luôn là trục đối xứng của đồ thị hàm số chẵn \(y = f(x)\)
Thật vậy, nếu điểm \(M(x ; y)\) thuộc đồ thị, tức là \(y = f(x)\) thì điểm đối xứng với M qua Oy là điểm \(M’(-x ; y)\) cũng thuộc đồ thị vì: \(f(-x) = f(x) = y\)
