Bài 1: Một ô tô tải khối lượng 5 tấn và một ô tô con khối lượng 1300kg chuyển động cùng chiều trên đường, chiếc trước chiếc sau với cùng vận tốc không đổi 54km/h. Tính:
a) Động năng của mỗi ô tô.
b) Động năng của ô tô con trong hệ quy chiếu gắn với ô tô tải.
Động năng của ô tô tải:
Wđ1\( = {{{m_1}{v^2}} \over 2} = {{{{5000.15}^2}} \over 2} = 562500(J)\)
Động năng ô tô con:
Wđ2\( = {{{m_2}{v^2}} \over 2} = {{{{1300.15}^2}} \over 2} = 146250(J)\)
b) Hai xe chuyển động cùng chiều, cùng vận tốc nên vận tốc của ô tô con trong hệ quy chiếu gắn với ô tô tải bằng 0\( \Rightarrow \)Wđ=0.
Bài 2: Một ô tô tăng tốc trong hai trường hợp: từ 10km/h lên 20km/h và từ 50km/h lên 60km/h trong cùng một khoảng thời gian như nhau. Nếu bỏ qua ma sát, hãy so sánh xem lực tác dụng và công do lực thực hiện trong hai trường hợp có bằng nhau không? Tại sao?
\( * \Delta {v_1} = \Delta {v_2};\Delta {t_1} = \Delta {t_2};\) m không đổi nên
\(\eqalign{ & {{m\Delta {v_1}} \over {\Delta {t_1}}} = {F_1} = {F_2} = {{m\Delta {v_2}} \over {\Delta {t_2}}} \cr & * \left. \matrix{ {A_1} = {m \over 2}\left[ {{{\left( {{{20} \over {3,6}}} \right)}^2} – {{\left( {{{10} \over {3,6}}} \right)}^2}} \right] \approx 11,6m(J) \hfill \cr {A_2} = {m \over 2}\left[ {{{\left( {{{60} \over {3,6}}} \right)}^2} – {{\left( {{{50} \over {3,6}}} \right)}^2}} \right] \approx 42,4m(J) \hfill \cr} \right\} \cr&\Rightarrow {A_1} \ne {A_2} \cr} \)
Lực tác dụng trong hai trường hợp bằng nhau.
Công do lực thực hiện trong hai trường hợp khác nhau.
Bài 3: Một viên đạn khối lượng m=10g bay ngang với vận tốc v1=300m/s xuyên qua tấm gỗ dày 5cm. Sau khi xuyên qua gỗ, đạn có vận tốc v2=100m/s. Tính lực cản trung bình của tấm gỗ tác dụng lên viên đạn.
Advertisements (Quảng cáo)
Độ dời điểm đặt lực bằng chiều dày tấm gỗ \(S=5cm=0,05m\).
Công của lực cản của gỗ tác dụng lên đạn:
\(A= -F.S = -0,05 F\) (J).
Độ biến thiên động năng khi qua tấm gỗ:
\(\Delta \)W’đ\( = {m \over 2}(v_2^2 – v_1^2) = {{0,01} \over 2}({100^2} – {300^2}) = – 400(J)\)
Áp dụng định lý động năng:
A=\(\Delta \)Wđ \( \Leftrightarrow – 0,05{F_C} = – 400\)
Độ lớn lực cản trung bình: FC = 8000(N).
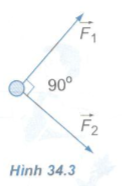
Bài 4: Trên mặt phẳng nhẵn nằm ngang, vật chịu tác dụng của hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) trong mặt phẳng và có phương vuông góc với nhau (Hình 34.3).
Khi vật dịch chuyển được 2m từ trạng thái nghỉ, động năng của vật bằng bao nhiêu? Xét các trường hợp:
a) F1=10N, F2=0.
Advertisements (Quảng cáo)
b) F1=0, F2=5N.
c) F1= F2 = 5N.
a) F1=10N; F2=0;
Vật chuyển động theo \(\overrightarrow {{F_1}} \)
\(\eqalign{ & \Rightarrow {A_1} = {F_1}.S = 20J. \cr & {v_0} = 0 \cr} \)
nên Wđ0 = 0 \(=>\) Wđ =∆Wđ = A1 = 20 J.
b) \({F_1} = 0;{F_2} = 5N.\)
Vật chuyển động theo \(\overrightarrow {{F_2}} \)
\( \Rightarrow {A_2} = {F_2}S = 10J \Rightarrow {{\rm{W}}_đ} = 10J.\)
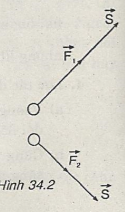
c) \({F_1} = {F_2} = 5N \Rightarrow \) hợp lực \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \) có độ lớn \(F = 5\sqrt 2 N\)
Vật chuyển động theo hợp lực \(\overrightarrow F \) nên:
\(A = F.S = 10\sqrt 2 \;J \Rightarrow {{\rm{W}}_đ} = 10\sqrt 2 \;J.\)
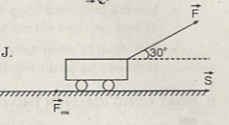
Bài 5: Một chiếc xe được kéo từ trạng thái nghỉ trên một đoạn đường nằm ngang dài 20m với một lực có độ lớn không đổi bằng 300N và có phương hợp với độ dời góc 300. Lực cản do ma sát cũng được coi là không đổi và bằng 200N. Tính công của mỗi lực. Động năng của xe ở cuối đoạn đường bằng bao nhiêu?
\(\eqalign{ & {v_0} = 0 \Rightarrow {{\rm{W}}_{d0}} = 0;S = 20m; \cr & F = 300N;{F_{ms}} = 200N \cr & {A_{ms}} = – {F_{ms}}.S = – 200.20 = – 4000J. \cr & {A_F} = F.S.\cos {30^0} = 300.20.{{\sqrt 3 } \over 2} = 3000\sqrt 3 J \cr & {{\rm{W}}_d} = \Delta {{\rm{W}}_d} = {A_F} + {A_{ms}} = 3000\sqrt 3 – 4000 \cr&\;\;\;\;\;\;\,\approx 1196J. \cr} \)
Bài 6: Một ô tô có khối lượng là 1600kg đang chạy với vận tốc 50km/h thì người lái nhìn thấy một vật cản trước mặt cách khoảng 15m. Người đó đang tắt máy và hãm phanh khẩn cấp. Giả sử lực hãm ô tô là không đổi và bằng 1,2.104N. Hỏi xe có kịp dừng tránh khỏi đâm vào vật cản hay không?
\(m = 1600kg;{v_0} = 50km/h = {{50} \over {3,6}}(m/s);l = 15m;\)
\({F_h} = 1,{2.10^4}N.\)
Áp dụng định lý động năng ta có: \(\eqalign{ & – {{\rm{W}}_{đ0}} = {A_h} \Leftrightarrow – {{mv_0^2} \over 2} = – {F_h}.S \cr & \Rightarrow S = {{mv_0^2} \over {2{F_h}}} = {{1600} \over {2.1,{{2.10}^4}}}.{\left( {{{50} \over {3,6}}} \right)^2} \approx 12,86(m). \cr & \Rightarrow S < l \cr} \)
Xe dừng kịp để không đâm vào vật cản.

