Câu 5: Tứ diện \(ABCD\) có hai mặt \(ABC\) và \(ADC\) nằm trong hai mặt phẳng vuông góc với nhau. Tam giác \(ABC\) vuông tại \(A\) có \(AB = a, AC = b\). Tam giác \(ADC\) vuông tại \(D\) có \(CD = a\).
a) Chứng minh các tam giác \(BAD\) và \(BDC\) đều là tam giác vuông
b) Gọi \(I\) và \(K\) lần lượt là trung điểm của \(AD\) và \(BC\). Chứng minh \(IK\) là đoạn vuông góc chung của hai đường thẳng \(AD\) và \(BC\).
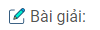
 ‘
‘
a) \((ABC) ⊥ (ADC)\) mà hai mặt phẳng này giao nhau theo giao tuyến \(AC\).
Ta lại có \(BA ⊂ (ABC)\) và \(BA⊥ AC\) nên \(BA⊥(ADC)\)
\(BA⊥(ADC) ⇒ BA⊥AD ⇒ ΔBAD\) vuông tại \(A\)
\(\left. \matrix{
BA \bot (ADC) \hfill \cr
AD \bot DC \hfill \cr} \right\} \Rightarrow BD \bot DC\)
(Định lí 3 đường vuông góc)
\(⇒ ΔBDC\) vuông tại \(D\)
b) Gọi \(J\) là trung điểm của \(AC\)
Ta có \(KJ//BA\)
Mà \(BA⊥(ADC) ⇒ KJ ⊥(ADC)\)
\( ⇒ KJ ⊥ AD\) (1)
Ta cũng có \(IJ//DC ⇒ IJ ⊥ AD\) (2)
Từ (1) và (2) suy ra: \(AD⊥(KIJ)\)
\(⇒ AD ⊥ IK\)
Ta lại có: \(ΔBAI = ΔCDI ⇒ IB = IC\)
\(⇒ ΔBIC\) cân đỉnh \(I ⇒ IK ⊥ BC\) (4)
Từ (3) và (4) suy ra \(IK\) là đoạn vuông góc chung của \(AD\) và \(BC\).
Câu 6: Cho hình lập phương \(ABCD.A’B’C’D’\) cạnh \(a\).
a) Chứng minh \(BC’\) vuông góc với mặt phẳng \((A’B’C’D)\)
b) Xác định và tính độ dài đoạn vuông góc chung của \(AB’\) và \(BC’\)
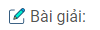
Advertisements (Quảng cáo)
a) Ta có tứ giác \(BCC’B’\) là hình vuông nên
\(BC’ ⊥ B’C\) (1)
Mặt khác \(A’B’ ⊥ (BCC’B’)\)
\(⇒ A’B’ ⊥ BC’\) (2)
Từ (1) và (2) suy ra: \(BC’⊥ (A’B’C’D’)\)
b) Do \(AD’//BC’\) nên mặt phẳng \((AB’D’)\) là mặt phẳng chứa \(AB’\) và song song với \(BC’\).
Ta tìm hình chiếu của \(BC’\) trên \(mp (AB’D’)\)
Gọi \(E, F\) là tâm của các mặt bên \(ADD’A’\) và \(BCC’B’\)
Từ \(F\) kẻ \(FI ⊥ B’E\). Ta có \(BC’ //AD’\) mà \(BC’ ⊥ (A’B’CD)\)
\(⇒ AD’ ⊥ (A’B’CD)\) và \(IF ⊂(A’B’CD)\)
\(AD’ ⊥ IF\) (3)
\(EB’⊥IF\) (4)
Từ (3) và (4) suy ra : \(IF ⊥ (AB’D’)\)
Vậy \(I\) là hình chiếu của \(F\) trên \(mp (AB’D’)\). Qua \(I\) ta dựng đường thẳng song song với \(BC’\) thì đường thẳng này chính là hình chiếu của \(BC’\) trên mp \((AB’D’)\)
Advertisements (Quảng cáo)
Đường thẳng qua \(I\) song song với \(BC’\) cắt \(AB’\) tại \(K\). Qua \(K\) kẻ đường thẳng song song với \(IF\), đường này cắt \(BC’\) tại \(H\). \(KH\) chính là đường vuông góc chung của \(AB’\) và \(BC’\). Thật vậy:
\({\rm{IF}} \bot (AB’D’)\)
\(\Rightarrow IF ⊥ AB’\) và \(KH // IF\) suy ra \(KH ⊥ AB’\)
\(\left. \matrix{
BC’ \bot (A’B’CD) \hfill \cr
{\rm{IF}} \subset {\rm{(A’B’CD)}} \hfill \cr} \right\} \Rightarrow \left. \matrix{
{\rm{IF}} \bot {\rm{BC’}} \hfill \cr
{\rm{KH//IF}} \hfill \cr} \right\} \Rightarrow KH \bot BC’\)
Tam giác \(EFB’\) vuông góc tại \(F\), \(FI\) là đường cao thuộc cạnh huyền nên
\({1 \over {I{F^2}}} = {1 \over {FB{‘^2}}} + {1 \over {F{E^2}}}\) với
\(\left\{ \matrix{
FB’ = {{a\sqrt 2 } \over 2} \hfill \cr
{\rm{EF = a}} \hfill \cr} \right.\)
Ta tính ra: \({\rm{IF}} = {{a\sqrt 3 } \over 3} \Rightarrow KH = {\rm{IF = }}{{a\sqrt 3 } \over 3}\)
Câu 7: Cho hình chóp \(S.ABCD\) có đáy là hình thoi \(ABCD\) cạnh \(a\), góc \(\widehat {BAD} = 60^0\) và \(SA = SB = SD = {{a\sqrt 3 } \over 2}\)
a) Tính khoảng cách từ \(S\) đến mặt phẳng \((ABCD)\) và độ dài cạnh \(SC\)
b) Chứng minh mặt phẳng \((SAC)\) vuông góc với mặt phẳng \((ABCD)\)
c) Chứng minh \(SB\) vuông góc với \(BC\)
d) Gọi \(\varphi\) là góc giữa hai mặt phẳng \((SBD)\) và \((ABCD)\). Tính \(\tan\varphi\)
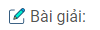
a) Kẻ \(SH⊥(ABCD)\)
Do \(SA = SB = SD\) suy ra \(HA = HB = HC\)
\(⇒ H\) là tâm đường tròn ngoại tiếp tam giác \( ABD\).
Do \(AB = AD = a\) và \(\widehat{ BAD} = 60^0\) nên tam giác \(ABD\) là tam giác đều cạnh \(a\),
Ta có:
\(\eqalign{
& AO = {{a\sqrt 3 } \over 2} \cr
& AH = {2 \over 3}AO \Rightarrow AH = {{a\sqrt 3 } \over 3} \cr} \)
Trong tam giác vuông \(SAH\), ta có: \(SA = {{a\sqrt 3 } \over 2};AH = {{a\sqrt 3 } \over 3}\)
Tính ra: \(SH = {{a\sqrt {15} } \over 6}\)
Ta cũng có: \(HC = {{2a\sqrt 3 } \over 3}\)
Trong tam giác vuông \(SHC\):
\(S{C^2} = S{H^2} + H{C^2}\)
Do đó ta tính được:
\(SC = {{a\sqrt 7 } \over 2}\)
b)
\(\left. \matrix{
SH \bot (ABCD) \hfill \cr
SH \subset (SAC) \hfill \cr} \right\} \Rightarrow (SAC) \bot (ABCD)\)
c) Ta có:
\(\eqalign{
& S{C^2} = {{7{a^2}} \over 4}(1) \cr
& B{C^2} = {a^2}(2) \cr
& S{B^2} = {{3{a^2}} \over 4}(3) \cr} \)
Từ (1), (2) và (3) ta có: \(S{C^2} = B{C^2} + S{B^2}\)
Theo định lí Pytago đảo, tam giác \(SBC\) vuông tại \(B\).
d) Ta có:
\(\eqalign{
& \left. \matrix{
DB \bot AC \hfill \cr
SH \bot (ABCD) \Rightarrow SH \bot DB \hfill \cr} \right\} \Rightarrow DB \bot (SAC) \cr
& \Rightarrow \left\{ \matrix{
DB \bot {\rm{OS}} \hfill \cr
{\rm{DB}} \bot AC \hfill \cr} \right. \cr} \)
Suy ra: \(\widehat{ SOH}\) là góc giữa hai mặt phẳng \((SBD)\) và \((ABCD)\)
Ta có:
\(\eqalign{
& \widehat{ SOH} = \varphi \cr
& \tan \varphi = {{SH} \over {OH}} \Rightarrow \tan \varphi = \sqrt 5 \cr} \)

