Câu 6: Nhắc lại định nghĩa:
a) góc giữa đường thẳng và mặt phẳng
b) góc giữa hai mặt phẳng
a) góc giữa đường thẳng và mặt phẳng
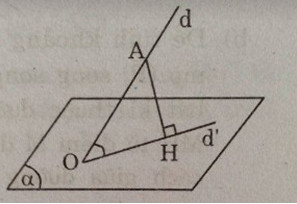
Định nghĩa: Cho đường thẳng \(d\) cắt mặt phẳng \((α)\) tại điểm \(O\) và không vuông góc với \((α)\). Góc giữa đường thẳng \(d\) và mặt phẳng \((α)\) là góc tạo bởi đường thẳng và hình chiếu vuông góc \(d’\) của \(d\) trên mp \((α)\).
b) Góc giữa hai mặt phẳng
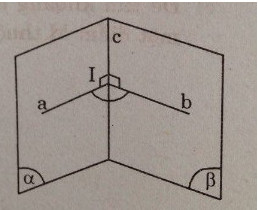
Định nghĩa: giả sử hai mặt phẳng \((α)\) và \((β)\) cắt nhau theo giao tuyến \(c\). Từ điểm \(I\) bất kì trên \(c\), trong mặt phẳng \((α)\) ta dựng đường thẳng \(a\) vuông góc với \(c\) và trong mặt phẳng \((β)\) ta dựng đường thẳng \(b\) vuông góc với \(c\). Ta gọi góc giữa hai đường thẳng \(a\) và \(b\) là góc giữa hai mặt phẳng \((α)\) và \((β)\).
Chú ý: góc giữa hai mặt phẳng luôn luôn nhỏ hơn hoặc bằng \(90^0\).
Câu 7: Muốn chứng minh mặt phẳng \((α)\) vuông góc với mặt phẳng \((β)\) người ta thường làm như thế nào?
Muốn chứng minh mặt phẳng \((α)\) vuông góc với mặt phẳng \((β)\), ta có thể:
Advertisements (Quảng cáo)
_ Chứng minh \((α)\) chứa một đường thẳng vuông góc với \((β)\) hoặc \((β)\) chứa một đường thẳng vuông góc với \((α)\)
\(\left\{ \matrix{
d \subset (\alpha ) \hfill \cr
d \bot (\beta ) \hfill \cr} \right. \Rightarrow (\alpha ) \bot (\beta )\)
_ Hoặc chứng minh góc giữa \((α)\) và \((β)\) bằng \(90^0\).
Câu 8: Hãy nêu cách tính khoảng cách:
a) Từ một điểm đến một đường thẳng
b) Từ đường thẳng \(a\) đến mặt phẳng \((α)\) song song với \(a\)
c) giữa hai mặt phẳng song song.
Advertisements (Quảng cáo)
a)
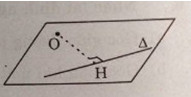
Để tính khoảng cách từ điểm \(O\) đến đường thẳng \(Δ\) không đi qua \(O\), ta xác định mặt phẳng \((O,Δ)\) và trong mặt phẳng này kẻ \(OH ⊥ Δ\). Độ dài \(OH\) chính là khoảng cách từ \(O\) đến \(Δ\).
b)
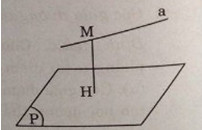
Để tính khoảng cách giữa đường thẳng \(a\) và mp \((P)\) song song với \(a\), ta lấy một điểm \(M\) bất kì thuộc đường thẳng \(a\). Khoảng cách \(MH\) từ điểm \(M\) đến mp \((P)\) chính là khoảng cách giữa đường thẳng \(a\) với mp \((P)\) song song với \(a\).
c)
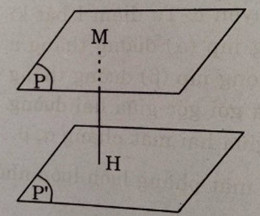
Để tìm khoảng cách giữa hai mp \((P)\) và \((P’)\) song song với nhau, ta lấy một điểm \(M\) thuộc \((P)\) và tìm khoảng cách \(MH\) từ điểm \(M\) đến mặt phẳng \((P’)\)
Câu 9: Cho \(a\) và \(b\) là hai đường thẳng chéo nhau. Có thể tính khoảng cách giữa hai đường thẳng chéo nhau bằng cách nào?
_ Dựng mặt phẳng \((P)\) qua \(a\) và song song với \(b\)
_ Tìm khoảng cách từ một điểm \(M\) thuộc \(b\) đến mặt phẳng \((P)\).
Câu 10: Chứng minh rằng tập hợp các điểm cách đều ba đỉnh của một tam giác \(ABC\) là đường vuông góc với mặt phẳng \((ABC)\) và đi qua tâm đường tròn ngoại tiếp tam giác \(ABC\).
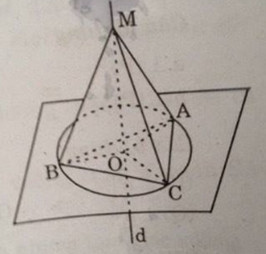
Lấy một điểm \(M\) bất kì trong không gian sao cho \(MA = MB = MC\). Từ \(M\) kẻ \(MO\) vuông góc với \((ABC)\). Các tam giác vuông \(MOA\), \(MOB\), \(MOC\) bằng nhau, suy ra \(OA = OB = OC\).
Do đó \(O\) là tâm đường tròn ngoại tiếp tam giác \(ABC\). Vậy các điểm \(M\) cách đều ba đỉnh của tam giác \(ABC\) nằm trên đường thẳng \(d\) đi qua tâm \(O\) của đường tròn ngoại tiếp tam giác \(ABC\) và vuông góc với mặt phẳng \((ABC)\). Ngược lại, lấy một điểm \(M’ ∈ d\), nối \(M’A, M’B, M’C\),
Do \(M’O\) chung và \(OA = OB = OC\) nên các tam giác vuông \(M’OA, M’OB, M’OC\) bằng nhau, suy ra \(M’A = M’B = M’C\),
Tức là điểm \(M’\) cách đều ba đỉnh \(A, B, C\) của tam giác \(ABC\).
Kết luận: Tập hợp các điểm cách đều ba đỉnh của tam giác \(ABC\) là đường thẳng vuông góc với mặt phẳng \((ABC)\) và đi qua tâm đường tròn ngoại tiếp tam giác \(ABC\).

