Câu 1: Cho hình lăng trụ tam giác \(ABC.A’B’C’\). Hãy kể tên những vecto bằng vecto \(\overrightarrow {AA’} \) có điểm đầu và điểm cuối là đỉnh của hình lăng trụ.
Vecto trong không gian là một đoạn thẳng có định hướng, tức là một đoạn thẳng đã được chỉ rõ điểm đầu và điểm cuối.
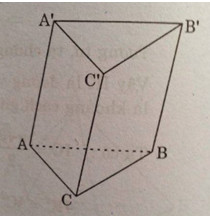
Vì các cạnh bên của hình lăng trụ là các đoạn thẳng song song và bằng nhau nên các vecto bằng vecto \(\overrightarrow {AA’} \) và có điểm đầu và điểm cuối là đỉnh của hình lăng trụ là: \(\overrightarrow {BB’} ,\overrightarrow {CC’} \)
Câu 2: Trong không gian cho ba vecto \(\overrightarrow a ,\overrightarrow b ;\overrightarrow c \) đều khác vecto \(\overrightarrow 0 \) . Khi nào ba vecto đó đồng phẳng?
Ba vecto \(\overrightarrow a ,\overrightarrow b ;\overrightarrow c \) đều khác vecto \(\overrightarrow 0 \) đồng phẳng khi và chỉ khi có cặp số \(m, n\) duy nhất sao cho:
Advertisements (Quảng cáo)
\(\overrightarrow c = m\overrightarrow a + n\overrightarrow b \)
Câu 3: Trong không gian, hai đường thẳng không cắt nhau có thể vuông góc với nhau không? Giả sử hai đường thẳng \(a\) và \(b\) lần lượt có vecto chỉ phương là \(\overrightarrow u \) và \(\overrightarrow v \) . Khi nào ta có thể kết luận \(a\) và \(b\) vuông góc với nhau?
Trong không gian, hai đường thẳng vuông góc với nhau không nhất thiết phải cắt nhau. Vì vậy hai đường thẳng không cắt nhau vẫn có thể vuông góc với nhau.
Đường thẳng \(a\) có vecto chỉ phương \(\overrightarrow u \)
Advertisements (Quảng cáo)
Đường thẳng \(b\) có vecto chỉ phương là \(\overrightarrow v \)
\(a\) vuông góc với \(b\) khi và chỉ khi tích vô hướng của hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) bằng không.
\(a \bot b \Leftrightarrow \overrightarrow u .\overrightarrow v = 0\)
Câu 4: Muốn chứng minh đường thẳng \(a\) vuông góc với mặt phẳng \((α)\) thì người ta cần chứng minh \(a\) vuông góc với mọi đường thẳng của mặt phẳng \(α\) hay không?
Muốn chứng minh đường thẳng \(a\) vuông góc với mặt phẳng \((α)\) thì người ta chỉ cần chứng minh \(a\) vuông góc với hai đường thẳng giao nhau của mặt phẳng \((α)\), lúc đó thì \(a ⊥( α)\)
\(\left\{ \matrix{
a \bot b,b \subset (\alpha ) \hfill \cr
a \bot c,c \subset (\alpha ) \hfill \cr
b \cap c \hfill \cr} \right. \Rightarrow a \bot (\alpha )\)
Câu 5: Hãy nhắc lại nội dung của định lí ba đường vuông góc
Định lí ba đường vuông góc:
Cho đường thẳng \(a\) nằm trong mặt phẳng \((α)\) và \(b\) là đường thẳng không thuộc \((α)\) đồng thời không vuông góc với \((α)\). Gọi \(b’ \) là hình chiếu của \(b\) trên \((α)\). Khi đó \(a\) vuông góc với \(b\) khi và chỉ khi \(a\) vuông góc với \(b’\).

