Bài 1: Cho ba mặt phẳng \((\alpha)\), \((\beta )\), \((\gamma )\), mệnh đề nào sau đây đúng?
a) Nếu \((\alpha)\bot\beta\) và \((\alpha) // (\gamma)\) thì \((\beta)\bot(\gamma)\);
b) Nếu \((\alpha)\bot\beta\) và \((\alpha) \bot (\gamma)\) thì \((\beta)//(\gamma)\).
a) Đúng.
b) Sai.
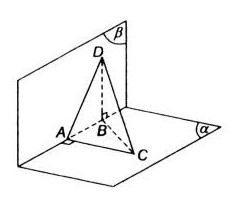
Bài 2: Cho hai mặt phẳng \((\alpha)\) và \((\beta)\) vuông góc với nhau. Người ta lấy trên giao tuyến \(\Delta\) của hai mặt phẳng đó hai điểm \(A\) và \(B\) sao cho \(AB=8cm\). Gọi \(C\) là một điểm trên \((\alpha)\) và \(D\) là một điểm trên \((\beta)\) sao cho \(AC\) và \(BD\) cùng vuông góc với giao tuyến \(\Delta\) và \(AC=6cm\), \(BD=24cm\). Tính độ dài đoạn \(CD\).
\(\left. \matrix{
(\alpha ) \bot (\beta ) \hfill \cr
AC \bot \Delta \hfill \cr
AC \subset (\alpha ) \hfill \cr} \right\} \Rightarrow AC \bot (\beta )\)
Do đó \(AC\bot AD\) hay tam giác \(ACD\) vuông tại \(A\)
Áp dụng định lí Pytago vào tam giác \(ACD\) ta được:
$$D{C^2} = A{C^2} + A{D^2}(1)$$
Advertisements (Quảng cáo)
Theo giả thiết \(BD\) vuông góc với giao tuyến nên \(BD\bot AB\) hay tam giác \(ABD\) vuông tại \(B\).
Áp dụng định lí Pytago vào tam giác \(ABD\) ta được:
$$A{D^2} = A{B^2} + B{D^2}(2)$$
Từ (1) và (2) suy ra: \(D{C^2} = A{C^2} + A{B^2} + B{D^2} = {6^2} + {8^2} + {24^2} = 676\)
\( \Rightarrow DC = \sqrt {676} = 26cm\)
Bài 3: Trong mặt phẳng \((\alpha)\) cho tam giác \(ABC\) vuông ở \(B\). Một đoạn thẳng \(AD\) vuông góc với \((\alpha)\) tại \(A\). Chứng minh rằng:
a) \(\widehat {ABD}\) là góc giữa hai mặt phẳng \((ABC)\) và \((DBC)\);
b) Mặt phẳng \((ABD)\) vuông góc với mặt phẳng \((BCD)\);
Advertisements (Quảng cáo)
c) \(HK//BC\) với \(H\) và \(K\) lần lượt là giao điểm của \(DB\) và \(DC\) với mặt phẳng \((P)\) đi qua \(A\) và vuông góc với \(DB\).
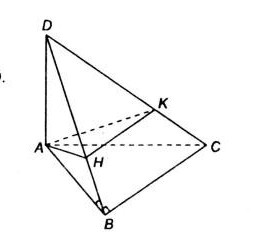
a) Tam giác \(ABC\) vuông tại \(B\) nên \(AB\bot BC\) (1)
\(AD\) vuông góc với \((\alpha)\) nên \(AD\bot BC\) (2)
Từ (1) và (2) suy ra \(BC\bot (ABD)\) suy ra \(BC\bot BD\)
\(\left. \matrix{
(ABC) \cap (DBC) = BC \hfill \cr
BD \bot BC \hfill \cr
AB \bot BC \hfill \cr} \right\} \Rightarrow \) góc giữa hai mặt phẳng \((ABC)\) và \((DBC)\) là góc \(\widehat {ABD}\)
b)
\(\left. \matrix{
BC \bot (ABD) \hfill \cr
BC \subset (BCD) \hfill \cr} \right\} \Rightarrow (ABD) \bot (BCD)\)
c)
Mặt phẳng \((P)\) đi qua \(A\) và vuông góc với \(DB\) nên \(HK\bot BC\)
Trong \((BCD)\) có: \(HK\bot BC\) và \(BC\bot BD\) nên suy ra \(HK// BC\).
Bài 4: Cho hai mặt phẳng \((\alpha)\), \((\beta)\) cắt nhau và một điểm \(M\) không thuộc \((\alpha)\) và không thuộc \((\beta)\). Chứng minh rằng qua điểm \(M\) có một và chỉ một mặt phẳng \((P)\) vuông góc với \((\alpha)\) và \((\beta)\). Nếu \((\alpha)\) song song với \((\beta)\) thì kết quả trên sẽ thay đổi như thế nào?
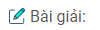
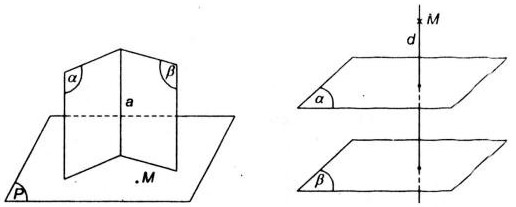
Gọi \(a=(\alpha)\cap (\beta)\). Mặt phẳng \((P)\) đi qua \(M\) và vuông góc với \(a\).
Vì \(a\subset (\alpha)\) nên \((P)\bot (\alpha)\), \(a\subset (\beta)\) nên \((P)\bot(\beta)\)
Như vậy qua \(M\) có mặt phẳng \((P)\) vuông góc với \((\alpha)\) và \((\beta)\).
Ngược lại: Nếu có \((P)\) đi qua \(M\) và vuông góc với \((\alpha)\) và \((\beta)\) thì \((P)\bot a\). Do tính duy nhất của mặt phẳng đi qua một điểm và vuông góc với một đường thẳng cho trước nên \((P)\) duy nhất.
Nếu \((\alpha)//(\beta)\) gọi \(d\) là đường thẳng đi qua \(M\) và vuông góc với \((\alpha)\) khi đó ta có \(d\bot (\beta)\). Như vậy mọi mặt phẳng chứa \(d\) đều vuông góc với \((\alpha)\) và \((\beta)\). Do đó khi \((\alpha)//(\beta)\) thì có vô số mặt phẳng \((P)\) đi qua \(M\) và vuông góc với \((\alpha)\) và \((\beta)\).

