Câu 1: Cho các cặp số và các phương trình sau. Hãy dùng mũi tên (như trong hình vẽ) chỉ rõ mỗi cặp số là nghiệm của phương trình nào:
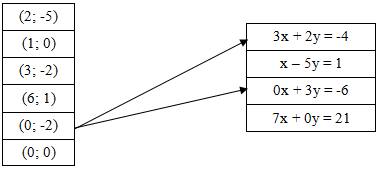
Câu 2: Viết nghiệm tổng quát và vẽ đường thẳng biểu diễn tập nghiệm của mỗi phương trình sau
a) \(2x – y = 3\)
b) \(x + 2y = 4\)
c) \(3x – 2y = 6\)
d) \(2x + 3y = 5\)
e) \(0x + 5y = – 10\)
f) \( – 4x + 0y = – 12\)
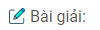
a) \(2x – y = 3\)\( \Leftrightarrow y = 2x – 3\) công thức nghiệm tổng quát (\(x \in R;y = 2x – 3\))
b) \(x + 2y = 4 \Leftrightarrow y = – {1 \over 2}x + 2\)
Công thức nghiệm tổng quát \((x \in R;y = – {1 \over 2}x + 2)\)
c) \(3x – 2y = 6 \Leftrightarrow y = {3 \over 2}x – 3\) công thức nghiệm tổng quát \((x \in R;y = {3 \over 2}x – 3)\)
d) \(2x + 3y = 5 \Leftrightarrow y = – {2 \over 3}x + {5 \over 3}\) công thức nghiệm tổng quát \(\left( {x \in R;y = – {2 \over 3}x + {5 \over 3}} \right)\)
e) \(0x + 5y = – 10 \Leftrightarrow y = – 2\) công thức nghiệm tổng quát \((x \in R;y = – 2)\)
f) \( – 4x + 0y = – 12 \Leftrightarrow x = 3\) công thức nghiệm tổng quát \((x = 3;y \in R)\)
Câu 3: Trong mỗi trường hợp sau hãy tìm giá trị của m để
a) Điểm M(1 ; 0) thuộc đường thẳng mx – 5y = 7
Advertisements (Quảng cáo)
b) Điểm N(0 ; -3) thuộc đường thẳng 2,5x + my = -21
c) Điểm P(5; -3) thuộc đường thẳng mx + 2y = -1
d) Điểm P(5; -3) thuộc đường thẳng 3x – my = 6.
e) Điểm Q(0,5; -3) thuộc đường thẳng mx + 0y = 17,5
f) Điểm S(4; 0,3) thuộc đường thẳng 0x + my = 1,5
g) Điểm A(2; -3) thuộc đường thẳng (m – 1)x + (m + 1)y = 2m + 1
a) Điểm M thuộc đường thẳng mx – 5y = 7 nên tọa độ của M phải nghiệm đúng phương trình đường thẳng
Ta có: \(m.1 – 5.0 = 7\)\( \Leftrightarrow m = 7\)
Vậy với m = 7 thì đường thẳng mx – 5y = 7 đi qua điểm \(M\left( {1;0} \right)\)
b) Điểm \(N\left( {0; – 3} \right)\) thuộc đường thẳng 2,5x + my = -21 đi qua điểm \(N\left( {0; – 3} \right)\)
Ta có: \(2,5.0 + m\left( { – 3} \right) = – 21\) \( \Leftrightarrow m = 7\)
Advertisements (Quảng cáo)
Vậy với m = 7 thì đường thẳng 2,5x + my = -21 đi qua \(N\left( {0; – 3} \right)\)
c) Điểm \(P\left( {5; – 3} \right)\) thuộc đường thẳng \(mx + 2y = – 1\) nên tọa độ của điểm P nghiệm đúng phương trình đường thẳng
Ta có: \(3.5 – m\left( { – 3} \right) = – 1\) \( \Leftrightarrow m = 1\)
Vậy với m = 1 thì đường thẳng \(mx + 2y = – 1\) đi qua điểm \(P\left( {5; – 3} \right)\)
d) Điểm \(P\left( {5; – 3} \right)\) thuộc đường thẳng \(3x – my = 6\) nên tọa độ của điểm P nghiệm đúng với phương trình đường thẳng
Ta có: \(3.5 – m\left( { – 3} \right) = 6 \Leftrightarrow 3m = – 9\) \( \Leftrightarrow m = – 3\)
Vậy với = – 3 thì đường thẳng \(3x – my = 6\) đi qua điểm \(P\left( {5; – 3} \right)\)
e) Điểm \(Q\left( {0,5; – 3} \right)\) thuộc đường thẳng mx + 0y = 17,5 nên tọa độ của điểm Q nghiệm đúng phương trình đường thẳng
Ta có: \(m.0,5 + 0.\left( { – 3} \right) = 17,5 \Leftrightarrow m = 35\)
Vậy với m = 35 thì đường thẳng mx + 0y = 17,5 đi qua điểm \(Q\left( {0,5; – 3} \right)\)
f) Điểm \(S\left( {4;0,3} \right)\) thuộc đường thẳng 0x + my = 1,5 nên tọa độ của điểm S nghiệm đúng phương trình đường thẳng
Ta có: \(0.4 + m.0,3 = 1,5 \Leftrightarrow m = 5\)
Vậy với m = 5 thì đường thẳng 0x + my = 1,5 đi qua điểm \(S\left( {4;0,3} \right)\)
g) Điểm \(A\left( {2; – 3} \right)\) thuộc đường thẳng \(\left( {m – 1} \right)x + \left( {m + 1} \right)y = 2m + 1\) nên tọa độ của điểm A nghiệm đúng phương trình đường thẳng
Ta có:
\(\eqalign{
& \left( {m – 1} \right).2 + \left( {m + 1} \right)\left( { – 3} \right) = 2m + 1 \cr
& \Leftrightarrow 2m – 2 – 3m – 3 = 2m + 1 \cr
& \Leftrightarrow 3m + 6 = 0 \cr
& \Leftrightarrow m = – 2 \cr} \)
Vậy với m = -2 thì đường thẳng \(\left( {m – 1} \right)x + \left( {m + 1} \right)y = 2m + 1\) đi qua điểm \(A\left( {2; – 3} \right)\).
Câu 4: Phương trình nào sau đây xác định 1 hàm số dạng y = ax + b?
a) 5x – y = 7 c) 3x + 5y = 10
b) 0x + 3y = -1 d) 6x – 0y = 18
a) \(5x – y = 7 \Leftrightarrow y = 5x – 7\) Xác định hàm số có dạng y = ax + b
Với a = 5 ; b = -7
b) \(3x + 5y = 10 \Leftrightarrow y = – {3 \over 5}x + 2\) Xác định hàm số có dạng y = ax + b
Với \(a = – {3 \over 5};b = 2\)
c) \(0x + 3y = – 1 \Leftrightarrow y = – {1 \over 3}\) Xác định hàm số có dạng y = ax + b
Với \(a = 0;b = – {1 \over 3}\)
d) \(6x – 0y = 18 \Leftrightarrow x = 3\) Không xác định hàm số có dạng y = ax + b

