Câu C1: Lăng kính trong phòng thí nghiệm là một khối lăng trụ có tiết diện chính là hình tam giác. Chọn góc nào là đính lăng kính?
Lăng kính trong phòng thí nghiệm là một khối lăng trụ có tiết diện chính là hình tam giác ABC, do đó ta có thể chọn góc nào là đỉnh lăng kính cũng được tuỳ theo thí nghiệm, như vậy ta có tất cả 3 góc chiết quang A,B và C.
Bài 1: Chọn phương án dứng.
Một tia sáng tới vuông góc với mặt AB của một lăng kính có chiết suất \(n = \sqrt 2 \) và góc ở đỉnh A = 30°, B là góc vuông. Góc lệch của tia sáng qua lăng kính là:
A. 5° B. 13°
C. 15° D. 22°
C là phương án đúng
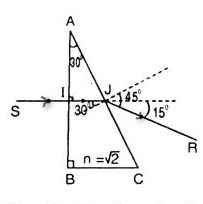
Ta có: \(i = {30^0} \Rightarrow {\mathop{\rm s}\nolimits} {\rm{inr}} = {{{n_1}\sin i} \over {{n_2}}}\)
\( \Rightarrow \sin r = {{\sqrt 2 \sin {{30}^0}} \over 1} = {{\sqrt 2 } \over 2} \Rightarrow r = {45^0}\)
Góc lệch D = 45° – 30° = 15°
Bài 2: Chọn phương án đúng.
Chiếu một chùm sáng song song tới lăng kính. Cho góc tới i tăng dần từ giá trị nhỏ nhất thỉ:
A. góc lệch D tăng theo i
B. góc lệch D giảm dần.
C. góc lệch D tăng tới một giá trị xác định rồi giảm dần.
D. góc lệch D giảm tới một giá trị xác định rồi tăng dần.
D là phương án đúng.
Bài 3: Phát biểu nào dưới đây không chính xác?
Chiếu một chùm tia sáng vào một mặt bên của một lăng kính ở trong không khí:
A. góc khúc xạ r bé hơn góc tới i.
B. góc tới r’ tại mặt bên thứ hai bé hơn góc ló i’
C. luôn luôn có chùm tia sáng ló ra ở mặt bên thứ hai.
D. Chùm tia sáng bị lệch khi đi qua lăng kính.
C là phát biểu không chính xác. Vì ta chỉ có chùm tia sáng ló ra ở mặt bên thứ hai nếu góc tới r’ nhỏ hơn góc giới hạn của lăng kính.
Bài 4: Khảo sát và vẽ đường di tia sáng trong trường hợp tia tới là là trên mặt lăng kính.
Trong trường hợp tia tới là là trên mặt lăng kính, ta có góc tới \(i \approx {90^0}\) theo công thức sini = nsinr
\(\Rightarrow {\mathop{\rm s}\nolimits} {\rm{inr}} = {{\sin i} \over n} = {{\sin {{90}^0}} \over n} = {1 \over n}\)
\(\Rightarrow \) r bằng góc giới hạn của lăng kính \(\Rightarrow \) r = igh.
Góc tới r’ = A – r = A – igh
Góc ló i’: \(sini'{\rm{ }} = {\rm{ }}nsinr'{\rm{ }} = {\rm{ }}nsin\left( {A{\rm{ }} – {\rm{ }}r} \right){\rm{ }}\)
\(= > {\rm{ }}sin\left( {A{\rm{ }} – {\rm{ }}r} \right){\rm{ }} = {\rm{ }}{1 \over n}{\rm{ }}sini’\)
Advertisements (Quảng cáo)
Dùng công thức lượng giác:
\(\sin A\cos r – \sin {\rm{rcosA = }}{{\sin i’} \over n}\)
\( \Leftrightarrow \sin A.\sqrt {1 – {\mathop{\rm s}\nolimits} {\rm{i}}{{\rm{n}}^2}{\rm{r}}} – \sin r\cos A = {{\sin i’} \over n}\)
\( \Leftrightarrow \sin A.\sqrt {1 – {1 \over {{n^2}}}} – {1 \over n}{\rm{cosA = }}{{\sin i’} \over n}\)
\( \Leftrightarrow \sin A.{{\sqrt {{n^2} – 1} } \over n} – {1 \over n}{\rm{cosA = }}{{\sin i’} \over n}\)
\( \Rightarrow \sin i’ = \sin A.\sqrt {{n^2} – 1} – c{\rm{osA}}\)
Từ đây ta tìm dược góc i’ và vẽ tia ló.
Bài 5: Một lăng kính thuỷ tinh có chiết suất n = 1,5; tiết diện chính là một tam giác đều, được đặt trong không khí.
a) Tính góc lệch của tia sáng qua lăng kính khi góc tới là 30°.
b) Vẽ đường đi tia sáng và tính góc mà tia ló hợp với tia tới trong trường hợp tia tới vuông góc với mặt bên của lăng kính.
a) Ta có A = 60°, n = 1,5; lăng kính đặt trong không khí.
Theo giả thiết i = 30° \(\Rightarrow {\mathop{\rm s}\nolimits} {\rm{inr}} = {{{\mathop{\rm s}\nolimits} {\rm{ini}}} \over n} = {{\sin {{30}^0}} \over {1,5}} = 0,333 \Rightarrow r = {19^0}28’\)
Ta có: r’ = A – r = 60 – 19°28′ = 40°32′
\(\Rightarrow\) \(\sin i’ = n\sin r’ \)= 1,5sin40°32′ = 0,975 \(\Rightarrow\) i’ = 77°
Vậy góc lệch D = i + i’ – A = 30° + 77° – 60° = 47°
b)
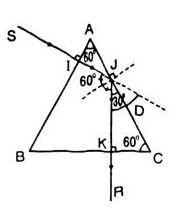
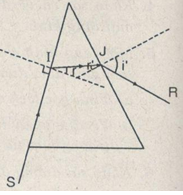
Trường hợp cho tia tới SI vuông góc với mặt bên lăng kính
Tia sáng đi từ không khí vào lăng kính:
n1= 1, n2 = 1,5
\(SI \bot AB\) \(\Rightarrow\) i = 0°
\( \Rightarrow {\mathop{\rm s}\nolimits} {\rm{inr}} = {{\sin i} \over n_2} = {0 \over {1,5}} = 0 \Rightarrow r = 0\)
Advertisements (Quảng cáo)
Tia IJ truyền thẳng đến mặt AC.
Tia sáng đi từ lăng kính ra không khí:
n1 = 1,5, n2 = 1
Ta có: \(\sin {i_{gh}} = {{{n_2}} \over {{n_1}}} = {1 \over {1,5}} \Rightarrow {i_{gh}} = {42^{0.}}\)
Góc tới i = 60° >igh nên có sự phản xạ toàn phần, tia JK là tia phản xạ.
Tia sáng đi từ lăng kính ra không khí: n1 = 1,5, n2 = 1
Ta có tia tới \(JK \bot BC\) nên i = 0 \(\Rightarrow\) r = 0
Tia ló KR truyền thẳng ra ngoài không khí
Dựa vào hinh vẽ ta tính được góc lệch D = 60°.
Bài 6: Khảo sát đường đi của tia sáng qua lăng kính trong hai trường hợp sau:
a) Lăng kính có góc ở đinh là A = 50°, chiết suất \(n = \sqrt 2 \) đặt trong nước có chiết suất \(n’ = {4 \over 3}\), góc tới là i = 45 .
b) Lăng kính thuỷ tinh đặt trong không khí có góc ở đính A = 75°, góc C = 60°, chiết suất n =1,5, góc tới của tia sáng là i = 30°. Tia tới đến mặt AB của lăng kính.
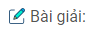
Khảo sát đường đi của tia sáng qua lăng kính
Ta giải theo phương pháp như sau:
1) Xét từng cặp môi trường tới (n1) và môi trường khúc xạ (n2).
Nếu n1< n2 : khúc xạ ánh sáng kiểu (cụp), vẽ r < i.
Nếu n1> n2: phải tính igh theo công thức \(\sin {i_{gh}} = {{{n_2}} \over {{n_1}}}\), sau đó so sánh với góc tới r’.
+ r’ < igh khúc xạ (kiểu xoè), vẽ r’ > r.
+ r’ = igh tia khúc xạ là là với mặt lăng kính.
+ r’ > igh phản xạ toàn phần, vẽ tia phản xạ với góc phản xạ bằng với góc tới r” = r’.
2) Lưu ý phải dùng thước đo góc chính xác để vẽ các tia sáng.
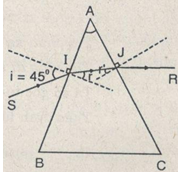
Câu a): Lăng kính có A = 50°,\(n = \sqrt 2 \)
đặt trong nước \(\left( {n’ = {4 \over 3}} \right)\), góc tới i = 450
Tia sáng đi từ nước \(\left( {{n_1} = {4 \over 3}} \right)\) \( \to \) lăng kính \(\left( {{n_2} = \sqrt 2 } \right)\)
Ta có: n1< n2, theo định luật khúc xạ ánh sáng
\({\mathop{\rm s}\nolimits} {\rm{inr}} = {{{n_1}\sin i} \over {{n_2}}} = {{{4 \over 3}\sin {{45}^0}} \over {\sqrt 2 }} \Rightarrow r = {41^0}48’\)
Tia khúc xạ là IJ đến mặt AC.
Tia sáng đi từ lăng kính \(\left( {{n_1} = \sqrt 2 } \right)\) \( \to \) nước \(\left( {{n_2} = {4 \over 3}} \right)\)
( n1 > n2 ) \(\Rightarrow\) Góc igh được tính \(\sin {i_{gh}} = {{{n_2}} \over {{n_1}}} = {{{4 \over 3}} \over {\sqrt 2 }} \Rightarrow {i_{gh}} = {70^0}31’\)
Góc tới r’ = A – r = 50° – 41°48′ = 8° 12′ < igh
Theo định luật khúc xạ ánh sáng:
\(\sin i’ = {{{n_1}{\mathop{\rm s}\nolimits} {\rm{inr}}’} \over {{n_2}}} = {{\sqrt 2 \sin {8^0}12′} \over {{4 \over 3}}} \Rightarrow i’ = {8^0}42’\)
Góc lệnh D = i + i’ – A = 45° + 8°42′ – 50 = 3°42′
Câu b)
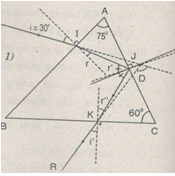
Lăng kính (n = 1,5) đặt trong không khí (n = 1); A = 75°, C = 60°, i = 30°.
Tia sáng đi từ không khí (n1= 1) vào lăng kính (n2 = 1,5), ta có n1< n2.
Theo định luật khúc xạ ánh sáng:
\(sinr = {{{n_1}\sin i} \over {{n_2}}} = {{\sin {{30}^0}} \over {1,5}}\)
\( \Rightarrow r = {19^0}30’\)
Tia khúc xạ là IJ đến mặt AC.
Tia sáng đi từ lăng kính (n1 = 1,5) vào không khí (n2 = 1), n1> n2
Ta có \(\sin {i_{gh}} = {{{n_2}} \over {{n_1}}} = {1 \over {1,5}} \Rightarrow {i_{gh}} = {42^0}\)
Góc tới r’ = A – r = 75° – 19°30′ = 55°30′
r’ > igh: phản xạ toàn phần.
Tia phản xạ JK trên mặt AC đến mặt BC.
Tia sáng đi từ lăng kính (n1= 1,5) vào không khí (n2 = 1)
Ta có góc tới r” = C – r’ = 60° – 55°30′ = 4°30′
Theo định luật khúc xạ ánh sáng:
\(\sin i’ = {{{n_1}\sin r”} \over {{n_2}}} = 1,5\sin {4^0}30′ \Rightarrow i’ = {6^0}45’\)
Tia ló KR như hình vẽ.
Góc lệch D = 81°45′
Bài 7: Lăng kính có góc ở đỉnh là 60°. Chùm sáng song song qua lăng kính có độ lệch cực tiểu là Dm = 42°. Hãy tìm góc tới và chiết suất của lăng kính.
Lăng kính có A = 60°, Dm = 42°. Tìm i và n
Áp dụng công thức: \(\sin {{{D_m} + A} \over 2} = n\sin {A \over 2}\)
Thay số:\(\sin {{{{60}^0} + {{42}^0}} \over 2} = n\sin {{{{60}^0}} \over 2} \Rightarrow n = {{\sin {{51}^0}} \over {\sin {{30}^0}}} = 1,55\)
Góc tới \(i = {{{D_m} + A} \over 2} = {{{{42}^0}+{{60}^0} } \over 2} = {51^0}\)

