Câu 12. Cho phép quay Q tâm O với góc quay \(\varphi \) và cho đường thẳng d. Hãy nêu cách dựng ảnh d’ của d qua phép quay Q
Giải
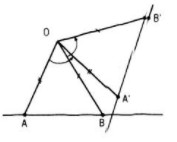
Ảnh d’ của đường thẳng d qua phép quay \(Q(O; φ)\) có thể dựng như sau:
Lấy hai điểm A, B phân biệt trên d, rồi dựng ảnh A’, B’ của chúng. Đường thẳng d’ là đường thẳng đi qua A’ và B’
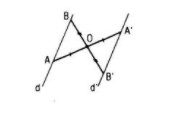
Câu 13. Cho hai tam giác vuông cân OAB và OA’B’ có chung đỉnh O sao cho O nằm trên đoạn thẳng A’B’ và nằm ngoài đoạn thẳng A’B (h.16). Gọi G và G’ lần lượt là trọng tâm các tam giác OAA’ và OBB’.Chứng minh GOG’ là tam giác vuông cân.
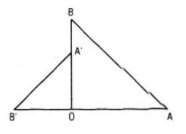
Giải
Gọi Q là phép quay tâm O, góc quay \({\pi \over 2}\) (bằng góc lượng giác (OA ; OB)). Khi đó Q biến A thành B và biến A’ thành B’, tức là biến tam giác OAA’ và OBB’
Bởi vậy Q biến G (trọng tâm tam giác OAA’) thành G’ (trọng tâm tam giác OBB’).
Suy ra \(OG = OG’\) và \(\widehat {GOG’} = {\pi \over 2}\)
Vậy GOG’ là tam giác vuông cân tại đỉnh O
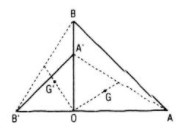
Chú ý: Phép quay Q biến trọng tâm G tam giác ABC thành trọng tâm G’ của tam giác A’B’C’ ảnh của △ABC qua Q được suy ra từ phép quay Q biến trung điểm I của đoạn thẳng
Câu 14. Giả sử phép đối xứng tâm \({D_O}\) biến đường thẳng d thành d’. Chứng minh
a. Nếu d không đi qua tâm đối xứng O thì d’ song song với d, O cách đều d và d’
b. Hai đường thẳng d và d’ trùng nhau khi và chỉ khi d đi qua O
Giải
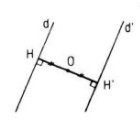
a. Kẻ \(OH ⊥ d (H ∈ d)\) thì vì d không đi qua O nên H không trùng với O
Phép đối xứng tâm \(Đ_ O\) biến H thành H’ thì O là trung điểm của HH’, và biến đường thẳng d thành đường thẳng d’ vuông góc với OH’ tại H’.
Suy ra d và d’ song song, cách đều điểm O
b. Nếu d không đi qua điểm O thì theo câu a), d’ // d nên d’ không trùng với d.
Nếu d đi qua O thì mọi điểm \(M ∈ d\) biến thành điểm \(M’ ∈ d’.\)
Advertisements (Quảng cáo)
Câu 15. Cho phép đối xứng tâm \({D_O}\) và đường thẳng d không đi qua O. Hãy nêu cách dựng ảnh d’ của đường thẳng d qua \({D_O}\). Tìm cách dựng d’ mà chỉ sử dụng compa một lần và thước thẳng ba lần
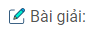
Cách dựng ảnh d’ của d như sau: Lấy hai điểm A, B phân biệt trên d rồi dựng ảnh A’, B’ của chúng. Đường thẳng d’ là đường thẳng đi qua A’ và B’
Ta có thể dựng cụ thể như sau: Dựng đường tròn \((O ; R)\) sao cho nó cắt d tại hai điểm phân biệt A, B. Dựng các đường thẳng AO và BO, chúng cắt đường tròn đó lần lượt tại A’ và B’
Dựng đường thẳng d’ đi qua A’ và B’
Phép dựng trên đây sử dụng compa một lần và thước thẳng ba lần
Câu 16. Chỉ ra tâm đối xứng của các hình sau đây:
a. Hình gồm hai đường thẳng cắt nhau
b. Hình gồm hai đường thẳng song song
c. Hình gồm hai đường tròn bằng nhau
d. Đường elip
e. Đường hypebol
Advertisements (Quảng cáo)
a. Tâm đối xứng là giao điểm của hai đường thẳng
b. Tâm đối xứng là những điểm cách đều hai đường thẳng
c. Tâm đối xứng là trung điểm của đoạn thẳng nối hai tâm đường tròn
d. Trung điểm của đoạn thẳng nối hai tiêu điểm của elip
e. Trung điểm của đoạn thẳng nối hai tiêu điểm của hypebol
Câu 17. Cho hai điểm cố định B, C trên đường tròn \((O; R)\) và một điểm A thay đổi trên đường tròn đó. Hãy dùng phép đối xứng tâm để chứng minh rằng trực tâm H của tam giác ABC nằm trên một đường tròn cố định
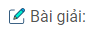Gọi I là trung điểm BC . Hãy vẽ đường kính AM của đường tròn rồi chứng minh rằng I là trung điểm của đoạn thẳng HM
Giải
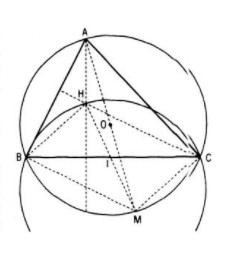
Ta vẽ đường kính AM của đường tròn. Khi đó BH // MC ( vì cùng vuông góc với AC) hay BHCM là hình bình hành
Nếu gọi I là trung điểm của BC thì I cố định và cũng là trung điểm của MH
Vậy phép đối xứng qua điểm I biến M thành H. Khi A chạy trên đường tròn \((O ; R)\) thì M chạy trên đường tròn \((O ; R)\). Do đó, H nằm trên đường tròn là ảnh của đường tròn \((O ; R)\) qua phép đối xứng tâm với tâm I
Câu 18. Cho đường tròn \((O; R)\) , đường thẳng \(△\) và điểm I . Tìm điểm A trên \((O; R)\) và điểm B trên \(△\) sao cho I là trung điểm của đoạn thẳng AB
Giải
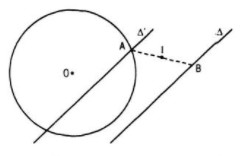
Giả sử ta đã có điểm A trên đường tròn \((O ; R)\) và điểm B trên △ sao cho I là trung điểm của đoạn thẳng AB
Phép đối xứng tâm ĐI biến điểm B thành điểm A nên biến đường thẳng \(△\) thành đường thẳng \(△’\) đi qua A.
Mặt khác A lại nằm trên \((O ; R)\) nên A phải là giao điểm của \(△’\) và \((O ; R)\)
Suy ra cách dựng:
Dựng đường thẳng \(△’\) là ảnh của \(△\) qua phép đối xứng tâm ĐI. Lấy A là giao điểm (nếu có) của \(△’\) và \((O ; R)\), còn B là giao điểm của đường thẳng AI và đường thẳng \(△\)
Câu 19. Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(\Delta :ax + by + c = 0\) và điểm \(I\left( {{x_0};{y_o}} \right)\). Phép đối xứng tâm \({D_I}\) biến đường thẳng \(△\) thành đường thẳng \(△’\). Viết phương trình của \(△’\)
Giải
Giả sử \(M (x , y) \in △\) và \(M’ (x’ , y ‘) \in △’\) và I là trung điểm của MM’ nên:
\(x + x’ = 2{x_0},\,\,y + y’ = 2{y_0} \Rightarrow \left\{ {\matrix{{x = 2{x_0} – x’} \cr {y = 2{y_0} – y’} \cr} } \right.\)
\(M(x , y) ∈△\) nên
\(\eqalign{
& a\left( {2{x_0} – x’} \right) + b\left( {2{y_0} – y’} \right) + c = 0 \cr
& \Leftrightarrow 2a{x_0} + 2b{y_0} – ax’ – by’ + c = 0 \cr
& \Leftrightarrow ax’ + by’ + c – 2\left( {a{x_0} + b{y_0} + c} \right) = 0 \cr} \)
Vậy M’ nằm trên đường thẳng ảnh \(△’\) có phương trình:
\(ax + by + c – 2(ax_0+ by_0+ c) = 0\)
