Câu 49. Tìm đạo hàm của các hàm số sau :
a. \(y = {{{x^4}} \over 2} + {{5{x^3}} \over 3} – \sqrt {2x} + 1\)
b. \(y = {{{x^2} + 3x – {a^2}} \over {x – 1}}\) (a là hằng số)
c. \(y = \left( {2 – {x^2}} \right)\cos x + 2x\sin x\)
d. \(y = {\tan ^2}x + \tan {x^2}\)
a. \(y’ = 2{x^3} + 5{x^2} – {1 \over {\sqrt {2x} }}\)
b. \(y’ = {{\left( {2x + 3} \right)\left( {x – 1} \right) – \left( {{x^2} + 3x – {a^2}} \right)} \over {{{\left( {x – 1} \right)}^2}}} = {{{x^2} – 2x + {a^2} – 3} \over {{{\left( {x – 1} \right)}^2}}}\)
c. \(y’ = – 2x\cos x – \left( {2 – {x^2}} \right)\sin x + 2\sin x + 2x\cos x \)
\(= {x^2}\sin x\)
d. \(y’ = 2\tan x\left( {1 + {{\tan }^2}x} \right) + 2x\left( {1 + {{\tan }^2}{x^2}} \right)\)
Câu 50. a. Chứng minh rằng \({\left( {{1 \over {{x^n}}}} \right)’} = – {n \over {{x^{n + 1}}}},\) trong đó n ϵ N*
b. Với x ≠ 0 và n ϵ N*, ta đặt \({x^{ – n}} = {1 \over {{x^n}}}.\) Từ đó hãy so sánh đẳng thức trong câu a với công thức \(\left( {{x^n}} \right)’ = n{x^{n – 1}}\) và nêu nhận xét.
a. Ta có: \(\left( {{1 \over {{x^n}}}} \right)’ = – {{\left( {{x^n}} \right)’} \over {{x^{2n}}}} = {{ – n{x^{n – 1}}} \over {{x^{2n}}}} = – {n \over {{x^{n + 1}}}}\)
b. Ta có: \(\left( {{x^{ – n}}} \right)’ = – n{x^{ – n – 1}}\) (Theo a)
Nhận xét : Công thức \(\left( {{x^n}} \right)’ = n{x^{n – 1}}\) đúng với mọi giá trị nguyên của n (chú ý rằng khi n ≤ 0 thì chỉ có thể xét đạo hàm trên \(\left( { – \infty ;0} \right) \cup \left( {0; + \infty } \right)\))
Câu 51. Tìm đạo hàm đến cấp được nêu kèm theo của các hàm số sau (n ϵ N*)
a. \(y=\sin x,\;y”’\)
b. \(y = \sin x\sin 5x,{y^{\left( 4 \right)}}\)
c. \(y = {\left( {4 – x} \right)^5},{y^{\left( n \right)}}\)
d. \(y = {1 \over {2 + x}},{y^{\left( n \right)}}\)
e. \(y = {1 \over {2x + 1}},{y^{\left( n \right)}}\)
f. \(y = {\cos ^2}x,{y^{\left( {2n} \right)}}\)
a.
\(\begin{array}{l}
y’ = \cos x\\
y” = – \sin x\\
y”’ = – \cos x
\end{array}\)
b.
\(\begin{array}{l}
y = \frac{1}{2}\left( {\cos 4x – \cos 6x} \right)\\
y’ = – 2\sin 4x + 3\sin 6x\\
y” = – 8\cos 4x + 18\cos 6x\\
y'” = 32\sin 4x – 108\sin 6x\\
{y^{\left( 4 \right)}} = 128\cos 4x – 648\cos 6x
\end{array}\)
c.
\(\begin{array}{l}
y’ = – 5{\left( {4 – x} \right)^4}\\
y” = 20{\left( {4 – x} \right)^3}\\
y”‘ = – 60{\left( {4 – x} \right)^2}\\
{y^{\left( 4 \right)}} = 120\left( {4 – x} \right)\\
{y^{\left( 5 \right)}} = – 120\\
{y^{\left( n \right)}} = 0\,\left( {\forall n \ge 6} \right)
\end{array}\)
d.
\(\begin{array}{l}
y = \frac{1}{{x + 2}} = {\left( {x + 2} \right)^{ – 1}}\\
y’ = – 1{\left( {x + 2} \right)^{ – 2}}\\
y” = \left( { – 1} \right)\left( { – 2} \right){\left( {x + 2} \right)^{ – 3}},…
\end{array}\)
Bằng qui nạp ta chứng minh được :
\({y^{\left( n \right)}} = \left( { – 1} \right)\left( { – 2} \right)…\left( { – n} \right).{\left( {x + 2} \right)^{ – n – 1}}\)
\(= {\left( { – 1} \right)^n}.\frac{{n!}}{{{{\left( {x + 2} \right)}^{n + 1}}}}\)
e.
\(\begin{array}{l}
y = {\left( {2x + 1} \right)^{ – 1}}\\
y’ = \left( { – 1} \right)\left( {2{{\left( {2x + 1} \right)}^{ – 2}}} \right)\\
y” = \left( { – 1} \right)\left( { – 2} \right){.2^2}{\left( {2x + 1} \right)^{ – 3}},…
\end{array}\)
Bằng qui nạp ta chứng minh được :
\({y^{\left( n \right)}} = {\left( { – 1} \right)^n}.\frac{{{2^n}.n!}}{{{{\left( {2x + 1} \right)}^{n + 1}}}}\)
f. Ta có:
\(\begin{array}{l}
y’ = – \sin 2x\\
y” = – 2\cos 2x\\
y”‘ = {2^2}\sin 2x\\
{y^{\left( 4 \right)}} = {2^3}\cos 2x\\
{y^{\left( 5 \right)}} = – {2^4}\sin 2x\\
{y^{\left( 6 \right)}} = – {2^5}\cos 2x,…
\end{array}\)
Bằng qui nạp ta chứng minh được :
\({y^{\left( {2n} \right)}} = {\left( { – 1} \right)^n}{.2^{2n – 1}}\cos 2x\)
Câu 52. Tính vi phân của hàm số \(y = {1 \over {{{\left( {1 + \tan x} \right)}^2}}}\) tại điểm \(x = {\pi \over 6}\) ứng với \(\Delta x = {\pi \over {360}}\) (tính chính xác đến hàng phần vạn).
Advertisements (Quảng cáo)
Ta có: \(df\left( x \right) = {{ – 2\left( {1 + \tan x} \right){1 \over {{{\cos }^2}x}}} \over {{{\left( {1 + \tan x} \right)}^4}}}.\Delta x = {{ – 2\Delta x} \over {{{\cos }^2}x{{\left( {1 + \tan x} \right)}^3}}}\)
Suy ra: \(df\left( {{\pi \over 6}} \right) = {{ – 2.{\pi \over {360}}} \over {{{\cos }^2}{\pi \over 6}{{\left( {1 + \tan {\pi \over 6}} \right)}^3}}} = {{ – \pi } \over {180.{3 \over 4}{{\left( {1 + {1 \over {\sqrt 3 }}} \right)}^3}}}\)
\(\approx – 0,0059\)
Câu 53. Gọi (C) là đồ thị của hàm số \(f\left( x \right) = {x^4} + 2{x^2} – 1\). Viết phương trình tiếp tuyến của (C) trong mỗi trường hợp sau :
a. Biết tung độ tiếp điểm bằng 2
b. Biết rằng tiếp tuyến song song với trục hoành
c. Biết rằng tiếp tuyến vuông góc với đường thẳng \(y = – {1 \over 8}x + 3\)
d. Biết rằng tiếp tuyến đi qua điểm A(0 ; -6)
a. \(f’\left( x \right) = 4{x^3} + 4x\) .Ta có \(2 = {y_0} = x_0^4 + 2x_0^2 – 1 \Leftrightarrow x_0^4 + 2x_0^2 – 3 = 0\)
\( \Leftrightarrow \left[ {\matrix{ {x_0^2 = 1} \cr {x_0^2 = – 3\,\left( \text{loại} \right)} \cr } \Leftrightarrow {x_0} = \pm 1} \right.\)
* Với x0 = 1 ta có \(f’\left( 1 \right) = {4.1^3} + 4.1 = 8\)
Phương trình tiếp tuyến trong trường hợp này là :
\(y – 2 = 8\left( {x – 1} \right) \Leftrightarrow y = 8x – 6\)
* Với x0 = -1 ta có \(f’\left( { – 1} \right) = 4.{\left( { – 1} \right)^3} + 4.\left( { – 1} \right) = – 8\)
Phương trình tiếp tuyến trong trường hợp này là :
\(y – 2 = – 8\left( {x + 1} \right) \Leftrightarrow y = – 8x – 6\)
b. Tiếp tuyến song song với trục hoành tại điểm có hoành độ x0 thỏa :
\(f’\left( {{x_0}} \right) = 0 \Leftrightarrow 4x_0^3 + 4{x_0} = 0 \Leftrightarrow 4{x_0}\left( {x_0^2 + 1} \right) = 0 \)
\(\Leftrightarrow {x_0} = 0\,\,\left( {{y_0} = – 1} \right)\)
Phương trình tiếp tuyến cần tìm là : \(y – \left( { – 1} \right) = 0\left( {x – 0} \right) \Leftrightarrow y = – 1\)
c. Vì tiếp tuyến phải tìm vuông góc với đường thẳng \(y = – {1 \over 8}x + 3,\) nên hệ số vuông góc của tiếp tuyến bằng 8, suy ra :
\(\eqalign{ & y’ = 8 \Leftrightarrow 4{x^3} + 4x – 8 = 0 \cr & \Leftrightarrow 4\left( {x – 1} \right)\left( {{x^2} + x + 2} \right) = 0 \Leftrightarrow x = 1 \cr} \)
Theo câu a, ta được phương trình tiếp tuyến phải tìm là : \(y = 8x – 6\)
d. Cách 1 : Phương trình tiếp tuyến tại điểm \(M\left( {{x_0};f\left( {{x_0}} \right)} \right)\) của đồ thị (C) là :
\(\eqalign{ & y = f’\left( {{x_0}} \right).\left( {x – {x_0}} \right) + f\left( {{x_0}} \right) \cr & \Leftrightarrow y = \left( {4x_0^3 + 4{x_0}} \right)\left( {x – {x_0}} \right) + x_0^4 + 2x_0^2 – 1 \cr} \)
Vì tiếp tuyến phải tìm đi qua điểm A(0 ; -6) nên ta có :
Advertisements (Quảng cáo)
\(\eqalign{ & – 6 = \left( {4x_0^3 + 4{x_0}} \right)\left( {0 – {x_0}} \right) + x_0^4 + 2x_0^2 – 1 \cr & \Leftrightarrow 3x_0^4 + 2x_0^2 – 5 = 0 \cr & \Leftrightarrow x_0^2 = 1\Leftrightarrow{x_0} = \pm 1 \cr} \)
Theo câu a, phương trình của hai tiếp tuyến cần phải tìm lần lượt là :
\(y = 8x – 6;\;y = – 8x -6\)
Cách 2 : Phương trình đường thẳng (1) đi qua điểm A(0 ; -6) với hệ số góc bằng k là : y = kx – 6
Để đường thẳng (1) là tiếp tuyến của đồ thị (C) (hay tiếp xúc với đồ thị (C)) thì ta phải tìm k sao cho :
\(\left\{ {\matrix{ {f\left( x \right) = kx – 6} \cr {f’\left( x \right) = k} \cr } } \right. \Leftrightarrow \left\{ {\matrix{ {{x^4} + 2{x^2} – 1 = kx – 6} \cr {4{x^3} + 4x = k} \cr } } \right.\)
Khử k từ hệ trên ta được : \(3{x^4} + 2{x^2} – 5 = 0 \Leftrightarrow {x^2} = 1 \Leftrightarrow x = \pm 1\)
Suy ra \(k = ± 8\).
Vậy hai tiếp tuyến phải tìm có phương trình là : \(y = 8x – 6;\;y = – 8x -6\)
Câu 54. Tìm một điểm trên đồ thị của hàm số \(y = {1 \over {x – 1}}\) sao cho tiếp tuyến tại đó cùng với các trục tọa độ tạo thành một tam giác có diện tích bằng 2.
Với mọi x ≠ 1, ta có : \(y’ = – {1 \over {{{\left( {x – 1} \right)}^2}}}\)
Phương trình tiếp tuyến của đồ thị đã cho tại điểm \({M_0}\left( {{x_0};{1 \over {{x_0} – 1}}} \right)\) (với \({x_0} \ne 1\) ) là : \(y = – {1 \over {{{\left( {{x_0} – 1} \right)}^2}}}\left( {x – {x_0}} \right) + {1 \over {{x_0} – 1}}\)
Tiếp tuyến này cắt trục hoành tại điểm A có
hoành độ xA thỏa mãn : \({{{x_A} – {x_0}} \over {{{\left( {{x_0} – 1} \right)}^2}}} = {1 \over {{x_0} – 1}} \Leftrightarrow {x_A} = 2{x_0} – 1\)
và cắt trục tung tại điểm B có tung độ yB là :
\({y_B} = {{{x_0}} \over {{{\left( {{x_0} – 1} \right)}^2}}} + {1 \over {{x_0} – 1}} = {{2{x_0} – 1} \over {{{\left( {{x_0} – 1} \right)}^2}}}\)
Ta có:
\(\eqalign{ & {S_{OAB}} = 2 \Leftrightarrow {1 \over 2}\left| {{x_A}} \right|.\left| {{y_B}} \right| = 2 \cr & \Leftrightarrow {{{{\left( {2{x_0} – 1} \right)}^2}} \over {{{\left( {{x_0} – 1} \right)}^2}}} = 4 \Leftrightarrow {x_0} = {3 \over 4} \cr} \)
Suy ra : \({y_0} = {1 \over {{3 \over 4} – 1}} = – 4.\) Vậy điểm phải tìm Mo có tọa độ là \(\left( {{3 \over 4}; – 4} \right)\)
Câu 55. Đồ thị (P) của một hàm số bậc hai y = P(x) đã bị xóa đi, chỉ còn lại trục đối xứng ∆, điểm A thuộc (P) và tiếp tuyến tại A của (P) (h. 5.8). Hãy tìm P(x) và vẽ lại đồ thị (P).
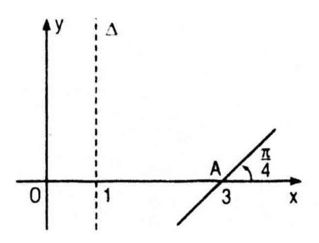
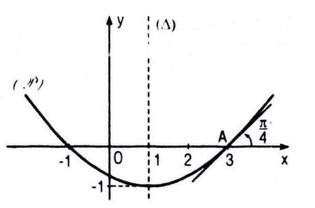
Đa thức phải tìm có dạng : \(P\left( x \right) = a{x^2} + bx + c\,\left( {a \ne 0} \right)\)
Ta có: \(P’\left( x \right) = 2ax + b\)
Vì trục đối xứng (∆) có phương trình x = 1 nên : \( – {b \over {2a}} = 1\,\,\left( 1 \right)\)
Vì đồ thị (P) đi qua điểm A(3 ; 0) nên ta có P(3) = 0, tức là:
\(9a + 3b + c = 0\,\,\left( 2 \right)\)
Vì hệ số góc của tiếp tuyến tại điểm A(3 ; 0) bằng \(\tan {\pi \over 4}\) nên ta có \(P’(3) = 1\), tức là :
\(6a + b = 1\,\left( 3 \right)\)
Giải hệ ba phương trình (1), (2) và (3) với ba ẩn số a, b và c, ta được :
\(\eqalign{ & a = {1 \over 4} \cr & b = – {1 \over 2} \cr & c = – {3 \over 4} \cr} \)
Vậy \(P\left( x \right) = {1 \over 4}{x^2} – {1 \over 2}x – {3 \over 4}\)
Câu 56. Cho parabol (P) : \(y = {x^2}.\) Gọi M1 và M2 là hai điểm thuộc (P), lần lượt có hoành độ là x1 = -2 và x2 = 1.
Hãy tìm trên (P) một điểm C sao cho tiếp tuyến tại C song song với cát tuyến M1M2. Viết phương trình của tiếp tuyến đó.
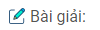
Các điểm M1 và M2 có tọa độ là M1(-2 ; 4); M2(1 ; 1)
Hệ số góc của cát tuyến M1M2 là \(\tan \varphi = {{\Delta y} \over {\Delta x}} = {{4 – 1} \over { – 2 – 1}} = – 1\)
Vì tiếp tuyến tại điểm \(C\left( {{x_0};x_0^2} \right)\) song song với cát tuyến M1M2 nên ta có :
\(y’\left( {{x_0}} \right) = – 1 \Leftrightarrow 2{x_0} = – 1 \Leftrightarrow {x_0} = {{ – 1} \over 2},\)
Suy ra tọa độ của điểm C là \(\left( { – {1 \over 2};{1 \over 4}} \right)\)
Vậy phương trình tiếp tuyến phải tìm là :
\(y = \left( { – 1} \right)\left( {x + {1 \over 2}} \right) + {1 \over 4} \Leftrightarrow y = – x – {1 \over 4}\)
Câu 57. Một chất điểm chuyển động có phương trình \(S = {t^3} – 3{t^2} – 9t + 2,\) ở đó, t > 0, t tính bằng giây (s) và S tính bằng mét (m)
a. Tính vận tốc tại thời điểm t = 2
b. Tính gia tốc tại thời điểm t = 3
c. Tính gia tốc tại thời điểm vận tốc bằng 0
d. Tính vận tốc tại thời điểm gia tốc bằng 0.
Ta có:
\(\begin{array}{l}
s’ = 3{t^2} – 6t – 9\\
s” = 6t – 6
\end{array}\)
a. Vận tốc tại thời điểm t = 2 là : v = s’(2) = -9 m/s
b. Gia tốc tại thời điểm t = 3 là : a = s”(3) = 12 m/s2
c.
\(\begin{array}{l}
v = s’ = 0 \Leftrightarrow 3{t^2} – 6t – 9 = 0 \Leftrightarrow t = 3\\
a\left( 3 \right) = s”\left( 3 \right) = 12\,m/{s^2}
\end{array}\)
d.
\(\begin{array}{l}
a = s” = 0 \Leftrightarrow 6t – 6 = 0 \Leftrightarrow t = 1\\
v\left( 1 \right) = s’\left( 1 \right) = – 12\,m/s
\end{array}\)

