Giải bài 1, 2, 3, 4, 5 trang 56 Toán lớp 6 tập 1 SGK Chân trời sáng tạo. Bài 2. Thứ tự trong tập hợp số nguyên – Chương 2 Số nguyên
Hoạt động khám phá 1

Nhiệt độ trung bình trong tháng Một tại hai địa điểm: Vostok (Vô-xtốc) và Ottawa (Ốt –ta- oa) lần lượt là \( – 31^\circ C\(và \( – 7^\circ C\(. Theo em, trong tháng Một, nơi nào lạnh hơn?
So sánh hai số âm và kết luận.

Ở Vô-xtốc lạnh hơn vì nhiệt độ ở đấy thấp hơn.
Thực hành trang 55 SGK Toán 6 CTST

So sánh các số nguyên sau:
a) \( – 10\( và \( – 9\(
b) \(2\( và \( – 15\(
c) 0 và \( – 3\(

a) \( – 10\( và \( – 9\( là các số nguyên âm.
Số đối của \( – 10\( là 10
Số đối của \( – 9\( là 9.
Do \(10 > 9\( nên \( – 10 < – 9\(.
b) \(2\( là số nguyên dương và \( – 15\(là số nguyên âm nên \(2 > – 15\(
c) \( – 3\( là số nguyên âm nên \( – 3\( luôn nhỏ hơn 0 \(\left( { – 3 < 0} \right)\(
Vận dụng 1

Cho ba số nguyên a, b, c và biết:
\(a > 2;b < – 7; – 1 < c < 1\(.
Hỏi trong các số nói trên, số nào là số nguyên dương, số nào là số nguyên âm và số nào bằng 0?
Biểu diễn các số trên trục số.
Số nào lớn hơn thì điểm biểu diễn số đó nằm bên phải số còn lại. Số nào nhỏ hơn thì điểm biểu diễn số đó nằm bên trái số còn lại.
Chỉ có duy nhất một số 0 là số nằm giữa -1 và 1.

\(a > 2\( nên a nằm bên phải số 2, số 2 lại nằm bên phải số 0 nên a nằm bên phải số 0. Vậy \(a > 0\( và là số nguyên dương.
\(b < – 7\( nên b nằm bên trái số \( – 7\( mà \( – 7\( nằm bên trái số 0 nên b nằm bên trái số 0. Vậy \(b < 0\( và là số nguyên âm.
\( – 1 < c < 1\( nên số c là số nằm giữa hai số -1 và 1. Mà chỉ có số 0 nằm giữa 2 số này nên c phải là số 0.
Hoạt động khám phá 2

Sắp xếp các số \( – 5;4; – 2;0;2\) theo thứ tự tăng dần.
Phân loại các số bài cho là số nguyên dương, số nguyên âm hay số 0.
Số nguyên âm nào có số đối lớn nhất thì sắp xếp trước. Sắp xếp xong số nguyên âm thì đến số 0. Sau đó sắp xếp số nguyên dương theo thứ tự tăng dần.

Advertisements (Quảng cáo)
Số nguyên âm là \( – 5; – 2\) do \(5 > 2 \Rightarrow – 5 < – 2\). Sắp xếp: \( – 5; – 2\).
Điền số 0 vào sau số -2: \( – 5; – 2\);0
Số nguyên dương: \(4 > 2\). Điền số 2 trước rồi đến số 4: \( – 5; – 2;0;2;4\)
Vận dụng 2

Một sinh vật biển sống gần mặt nước, trong khi đó một số khác lại sống rất sâu dưới đáy đại dương. Hãy sắp xếp các sinh vật biển sau theo thứ tự giảm dần độ cao của môi trường sống.


\(180 < 1000 < 4000 < 6000\)
\( \Rightarrow – 180 > – 1000 > – 4000 > – 6000\)
Thứ tự các sinh vật biển: Cá cờ xanh;Cá hố; Cá đèn; Sao biển.
Giải bài 1 trang 56 Toán 6 Chân trời sáng tạo tập 1

So sánh các cặp số sau:
a) 6 và 5; b) \( – 5\( và 0;
c) \( – 6\( và 5; d) \( – 8\( và \( – 6\(;
e) \(3\( và \( – 10\(; g) \( – 2\( và \( – 5\(
Phân loại các số bài cho là số nguyên dương, số nguyên âm hay số 0.
Áp dụng:
– Mọi số nguyên dương đều lớn hơn số 0.
– Mọi số nguyên âm đều nhỏ hơn số 0.
– Mọi số nguyên âm đều nhỏ hơn bất kì số nguyên dương nào.
Advertisements (Quảng cáo)
– Với hai số nguyên âm số nào có số đối lớn hơn thì số đó nhỏ hơn.

a) \(6 > 5\(
b) \( – 5\( là số nguyên âm nên \( – 5 < 0\(
c) \( – 6\( là số nguyên âm, 5 là số nguyên dương nên \( – 6 < 5\(
d) \( – 8\( và \( – 6\( là các số nguyên âm và có số đối lần lượt là 8 và 6.
\(8 > 6 \Rightarrow – 8 < – 6\(
e) 3 là số nguyên dương, \( – 10\( là số nguyên âm nên \(3 > – 10\(
g) \( – 2\( và \( – 5\( là các số nguyên âm có số đối lần lượt là 2 và 5.
\(2 < 5 \Rightarrow – 2 > – 5\(
Giải bài 2 trang 56 Toán lớp 6 Chân trời sáng tạo

Tìm số đối của các số nguyên: \(5; – 4; – 1;0;10; – 2021\(

Số đối của các số nguyên: \(5; – 4; – 1;0;10; – 2021\( lần lượt là \( – 5;4;1;0; – 10;2021\(
Giải Bài 3

Sắp xếp các số nguyên sau theo thứ tự tăng dần và biểu diễn chúng trên trục số:
\(2; – 4;6;4;8;0; – 2; – 8; – 6\(.

Số nguyên âm: \( – 4; – 2; – 8; – 6\(.
Số nguyên dương: \(2;4;6;8\(
Sắp xếp: \( – 8; – 6; – 4; – 2;0;2;4;6;8\(
Trục số:

Bài 4 trang 56 SGK Toán 6 tập 1 CTST

Hãy liệt kê các phần tử của mỗi tập hợp sau:
a) \(A = \left\{ {a \in \mathbb{Z}| – 4 < a < – 1} \right\}\(
b) \(B = \left\{ {b \in \mathbb{Z}| – 2 < b < 3} \right\}\(
c) \(C = \left\{ {c \in \mathbb{Z}| – 3 < c < 0} \right\}\(
d) \(A = \left\{ {d \in \mathbb{Z}| – 1 < d < 6} \right\}\(

a) \(A = \left\{ {a \in \mathbb{Z}| – 4 < a < – 1} \right\}\(
A là tập hợp các số nguyên a thỏa mãn \( – 4 < a < – 1\(.
\( – 4 < a < – 1\( có nghĩa là: a là số nguyên nằm giữa \( – 4\( và \( – 1\(. Có các số \( – 3; – 2\(.
Vậy \(A = \left\{ { – 3; – 2} \right\}\(
b) \(B = \left\{ {b \in \mathbb{Z}| – 2 < b < 3} \right\}\(
B là tập hợp các số nguyên b thỏa mãn \( – 2 < b < 3\(.
\( – 2 < b < 3\( có nghĩa là: b là số nguyên nằm giữa \( – 2\( và \(3\(. Có các số \( – 1;0;1;2\(.
Vậy \(B = \left\{ { – 1;0;1;2} \right\}\(
c) \(C = \left\{ {c \in \mathbb{Z}| – 3 < c < 0} \right\}\(
C là tập hợp các số nguyên c thỏa mãn \( – 3 < c < 0\(.
\( – 3 < c < 0\( có nghĩa là: c là số nguyên nằm giữa \( – 3\( và 0. Có các số \( – 2; – 1\(.
Vậy \(C = \left\{ { – 2; – 1} \right\}\(
d) \(D = \left\{ {d \in \mathbb{Z}| – 1 < d < 6} \right\}\(
D là tập hợp các số nguyên d thỏa mãn \( – 1 < d < 6\(.
\( – 1 < d < 6\( có nghĩa là: b là số nguyên nằm giữa \( – 1\( và 6. Có các số \(0;1;2;3;4;5\(.
Vậy \(D = \left\{ {0;1;2;3;4;5} \right\}\(
Giải bài 5 trang 56 SGK Toán 6 tập 1 Chân trời sáng tạo

Sắp xếp theo thứ tự từ thấp đến cao nhiệt độ \(\left( {^\circ C} \right)\) mùa đông tại các địa điểm sau đây của nước Mĩ: Hawaii (Ha-oai) \(12^\circ C\); Montana (Môn-ta-na) \( – 2^\circ C\); Alaska (A-la-xca) \( – 51^\circ C\); New York (Niu- Oóc) \( – 15^\circ C\); Florida (Phlo-ri-đa)\(8^\circ C\).

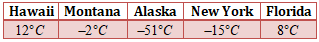
\(51 > 15 > 2 \Rightarrow – 51 < – 15 < – 2\)
Sắp xếp nhiệt độ: \( – 51^\circ C; – 15^\circ C; – 2^\circ C;8^\circ C;12^\circ C\)

