Câu 1. Trong các mệnh đề sau, mệnh đề nào đúng?
a. Hai đường thẳng chéo nhau thì không có điểm chung
b. Hai đường thẳng không có điểm chung thì chéo nhau
c. Hai đường thẳng chéo nhau thì không cùng thuộc một mặt phẳng
d. Hai đường thẳng không song song thì chéo nhau
a. Đúng
b. Sai: có thể a // b
c. Đúng
d. Sai: có thể a cắt b
Câu 2. Trong các mệnh đề sau, mệnh đề nào đúng ?
a. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau
b. Hai mặt phẳng phân biệt cùng song song với một đường thẳng thì song song với nhau
c. Hai mặt phẳng phân biệt không song song thì cắt nhau
d.Hai mặt phẳng phân biệt cùng song song với một mặt phẳng thứ ba thì song song với nhau
e. Một đường thẳng cắt một trong hai đường thẳng song song thì cắt đường thẳng còn lại
f. Một mặt phẳng cắt một trong hai đường thẳng song song thì cắt đường thẳng còn lại
g. Một đường thẳng cắt một trong hai mặt phẳng song song thì cắt mặt phẳng còn lại
a. Sai: có thể a cắt b hoặc a chéo b
b. Sai: có thể (α) và (β) cắt nhau
c. Đúng
d. Đúng
e. Sai: có thể cắt đường thứ nhất chéo nhau với đường thứ hai
f. Đúng
g. Đúng
Câu 3. Trong các hình sau, hình nào là hình biểu diễn của một tứ diện ?
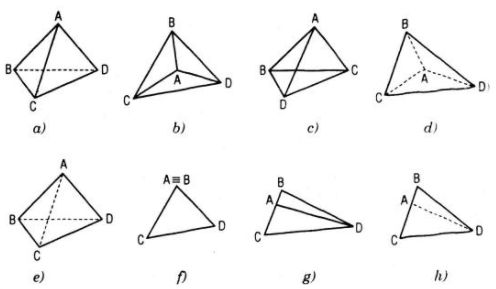
Các hình a, b, d, f, g, h
Câu 4. Cho hai hình bình hành ABCD VÀ ABEF nằm trong hai mặt phẳng khác nhau. Lấy các điểm M, N lần lượt thuộc các đường chéo AC, BF sao cho MC = 2AM, NF = 2BN. Qua M, N, kẻ các đường thẳng song song với AB cắt các cạnh AD, AF lần lượt tại M1, N1. Chứng minh rằng:
a. MN // DE
b. M1N1 // mp(DEF)
c. mp(MNN1M1) // mp(DEF)
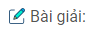
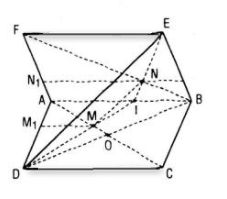
a. Gọi O là tâm hình bình hành ABCD, ta có AO là trung tuyến và \({{AM} \over {AO}} = {{2AM} \over {AC}} = {2 \over 3}\)
⇒ M là trọng tâm của tam giác ABD , tương tự N là trọng tâm tam giác ABE
Gọi I là trung điểm của AB thì M, N lần lượt trên DI và EI
Advertisements (Quảng cáo)
Trong tam giác IDE ta có: \({{IM} \over {ID}} = {{IN} \over {IE}} = {1 \over 3}\) nên MN // DE và \(MN = {1 \over 3}DE\)
b. Trong ∆FAB: NN1 // AB ⇒ \({{A{N_1}} \over {AF}} = {{BN} \over {BF}} = {1 \over 3}\)
Trong ∆DAB: MM1 // AB ⇒ \({{A{M_1}} \over {AD}} = {{DM} \over {DI}} = {1 \over 3}\)
Do đó \({{A{N_1}} \over {AF}} = {{A{M_1}} \over {AD}}\) nên M1N1 // DF
Mà DF ⊂ (DEF) suy ra M1N1 // mp(DEF)
c. Ta có : M1N1 // DF , NN1 // EF
mà M1N1 và NN1 cắt nhau và nằm trong mp(MNN1M1), còn DF và EF cắt nhau và nằm trong mp(DEF)
Vậy mp(MNN1M1) // mp(DEF)
Câu 5. Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC và A’B’C’. Một mặt phẳng (α) cắt các cạnh AA’, BB’, CC, GG’ lần lượt tại A1, B1, C1 và G1. Chứng minh rằng:
a. GG’ song song và bằng cạnh bên của hình lăng trụ
b. G1 là trọng tâm của tam giác A1B1C1
c. \({G_1}G’ = {1 \over 3}\left( {{A_1}A’ + {B_1}B’ + {C_1}C’} \right);\)
\({G_1}G = {1 \over 3}\left( {{A_1}A + {B_1}B + {C_1}C} \right)\)
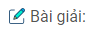
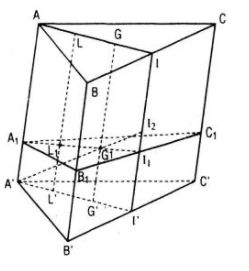
a. Gọi I, I’ lần lượt là trung điểm của các cạnh BC, B’C’ thì rõ ràng II’ song song và bằng AA’ nên tứ giác AII’A’ là hình bình hành, do đó AI song song và bằng A’I’
Ta cũng có \(AG = {2 \over 3}AI,A’G’ = {2 \over 3}A’I’\), mà AI = A’I’ suy ra AG song song và bằng A’G’
Vậy tứ giác AGG’A’ là hình bình hành
Do đó, GG’ song song và bằng AA’
b. B1C1 cắt II’ tại I1 thì I1 là trung điểm của B1C1
Vì G1 thuộc A1I1 và AA1 // GG1 // II1 nên \({{{G_1}{A_1}} \over {{A_1}{I_1}}} = {{GA} \over {AI}} = {2 \over 3}\)
Vậy G1 là trọng tâm tam giác A1B1C1
c. Xét hình bình hành AII’A’. Gọi L, L’ lần lượt là trung điểm của AG và A’G’, L1 là giao điểm của LL’ và A1I1
Khi đó L1 là trung điểm của A1G1
Theo định lí về đường trung bình của hình thang ta có :
\(2{G_1}G’ = {L_1}L’+{I_1}I’ = {1 \over 2}\left( {{A_1}A’ + {G_1}G’} \right) + {I_1}I’\)
Advertisements (Quảng cáo)
Suy ra: \({G_1}G’ = {1 \over 3}\left( {{A_1}A’ + 2{I_1}I’} \right)\)
Mặt khác: 2I1I’ = B1B’ + C1C’
Vậy: \({G_1}G’ = {1 \over 3}\left( {{A_1}A’ + {B_1}B’ + {C_1}C’} \right)\)
Chứng minh tương tự ta có: \({G_1}G = {1 \over 3}\left( {{A_1}A + {B_1}B + {C_1}C} \right)\)
Câu 6. Cho hình hộp ABCD.A’B’C’D’. Vẽ thiết diện của hình hộp tạo bởi mặt phẳng đi qua hai trung điểm M, N của các cạnh AB, AD và tâm O của mặt CDD’C’
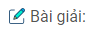
Gọi I và J lần lượt là các giao điểm của đường thẳng MN với BC và CD
Gọi P, Q lần lượt là các giao điểm của đường thẳng JO với các cạnh DD’, CC’
Gọi R là giao của BB’ và đường thẳng IQ. Ta có:
(MNO) ∩ (ABCD) = MN
(MNO) ∩ (CDD’C’) = PQ
(MNO) ∩ (ADD’A’) = NP
(MNO) ∩ (BCC’B’) = RQ
(MNO) ∩ (ABB’A’) = MR
Vậy thiết diện cần tìm là ngũ giác MNPQR
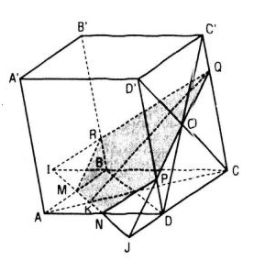
Câu 7. Cho hình hộp ABCD.A’B’C’D’. Trên ba cạnh AB, DD’, C’B’ lần lượt lấy ba điểm M, N, P không trùng với các đỉnh sao cho \({{AM} \over {AB}} = {{D’N} \over {D’D}} = {{B’P} \over {B’C’}}\)
a. Chứng minh rằng mp(MNP) và mp(AB’D’) song song với nhau
b. Xác định thiết diện của hình hộp khi cắt bởi mp(MNP)
a. Kẻ ME song song với AB’ (E ∈ BB’) (1)
Ta có: \(\eqalign{ & {{B’E} \over {B’B}} = {{AM} \over {AB}} \Rightarrow {{B’E} \over {B’B}} = {{B’P} \over {B’C’}} \cr & \cr} \)
⇒ EP // BC’ ⇒EP // AD’ (2)
Từ (1) và (2) suy ra (MEP) // (AB’D’) (3)
Rõ ràng D’N = B’E nên EN // B’D’
Mà B’D’ ⊂ (AB’D’) và E ∈ (MEP) nên từ (3) suy ra EN ⊂ (MEP), tức (MNP) chính là (MEP)
Vậy (MNP) // (AB’D’)
b. Từ M kẻ ME song song với AB’, từ P kẻ PF song song với B’D’. Từ N kẻ NK song song với AD’ cắt AD tại K
Thiết diện là lục giác MEPFNK có các cạnh đối song song
Câu 8. Cho hai tia Ax và By nằm trên hai đường thẳng chéo nhau. Một điểm M chạy trên Ax và một điểm N chạy trên By sao cho AM = kBN (k > 0 cho trước)
a. Chứng minh rằng MN song song với một mặt phẳng cố định
b. Tìm tập hợp các điểm I thuộc đoạn MN sao cho IM = kIN
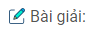
a.
Dựng tia Bz song song và cùng hướng với tia Ax. Trên các tia Ax, By và Bz lần lượt lấy các điểm cố định M0, N0 và M’0 sao cho \({{A{M_0}} \over {B{N_0}}} = k\) và \(BM{‘_0} = A{M_0}\)
Khi đó ta có : \({M_0}M{‘_0}//AB\) và \({{BM{‘_0}} \over {BN_0}} = k\,\,\left( 1 \right)\)
Lấy điểm M’ thuộc tia Bz sao cho BM’ = AM.
Từ (1) và (2) ta có : MM’ // M0M’0 (3)
Và \({{BM’} \over {BN}} = {{B{M’_0}} \over {B{N_0}}}\,\,\left( 4 \right)\)
Từ (4) suy ra NM’ // N0M’0 (5)
Từ (3) và (5) suy ra mp(MNM’) // mp(M0N0M’0).
Vậy MN luôn song song với mặt phẳng cố định (M0N0M’0)
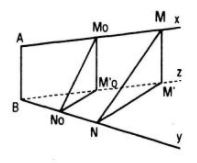
b.
Thuận. Gọi O là một điểm thuộc đoạn thẳng AB sao cho OA : OB = k. Từ O ta vẽ hai tia Ox’ và Oy’ sao cho Ox’ // Ax, Oy’ // By. Xét phép chiếu song song theo phương AB lên mp(Ox’, Oy’). Gọi M’, N’ lần lượt là hình chiếu của M và N theo phép chiếu này. Khi đó, giao điểm của MN và M’N’ chính là điểm I vì rõ ràng ta có :
\({{IM} \over {IN}} = {{M’M} \over {N’N}} = {{OA} \over {OB}} = k\)
Trong tam giác M’ON’, ta có : \({{IM’} \over {IN’}} = k,{{OM’} \over {ON’}} = {{AM} \over {BN}} = k\)
Vậy \({{IM’} \over {IN’}} = {{OM’} \over {ON’}} = k.\) Từ đó suy ra I phải nằm trên tia phân giác Ot của góc x’Oy’.
Đảo. Giả sử I là một điểm bất kì thuộc tia phân giác Ot của góc x’Oy’.
Gọi M’, N’ là những điểm lần lượt thuộc tia Ox’, tia Oy’ sao cho M’, I, N’ thẳng hàng và \({{IM’} \over {IN’}} = k\) (có thể tìm M’, N’ bằng cách dùng phép vị tự tâm I tỉ số -k trên mp(Ox’y’)). Gọi M, N lần lượt là những điểm thuộc các tia Ax, By sao cho AM = OM’, BN = ON’. Dễ thấy I, M, N thẳng hàng và IM : IN = k
Kết luận : Tập hợp các điểm I thỏa mãn điều kiện bài toán là tia phân giác Ot của góc x’Oy’.

