Câu 43. Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ?
a. Các hàm số \(y = \sin x, y = \cos x\) có cùng tập xác định.
b. Các hàm số \(y = \tan x, y = \cot x\) có cùng tập xác định.
c. Các hàm số \(y = \sin x, y = \tan x\) là những hàm số lẻ.
d. Các hàm số \(y = \cos x, y = \cot x\) là những hàm số chẵn.
e. Các hàm số \(y = \sin x, y = \cos x\) cùng nghịch biến trên khoảng \(\left( {{\pi \over 2};{{3\pi } \over 2}} \right)\)
f. Hàm số \(y = \cos x\) nghịch biến trên khoảng \((-2π ; -π)\)
g. Trên mỗi khoảng mà hàm số \(y = \tan x\) đồng biến thì hàm số \(y = \cot x\) nghịch biến.
a. Đúng vì hàm số \(y = \sin x, y = \cos x\) có cùng tập xác định \(D =\mathbb R\)
b. Sai vì \(y = \tan x\) xác định \(∀x \ne {\pi \over 2} + k\pi \) còn \(y = \cot x\) xác định \(∀x ≠ kπ\)
c. Đúng
d. Sai vì \(y = \cot x\) là hàm số lẻ.
e. Sai vì \(y = \cos x\) không nghịch biến trên khoảng \(\left( {{\pi \over 2};{{3\pi } \over 2}} \right)\)
f. Đúng
g. Sai vì trên khoảng \(\left( { – {\pi \over 2};{\pi \over 2}} \right)\) hàm số \(y = \tan x\) đồng biến nhưng hàm số \(y = \cot x\) không nghịch biến.
Câu 44. Xét hàm số \(y = f(x) = \sinπx\).
a. Chứng minh rằng với mỗi số nguyên chẵn \(m\) ta có \(f(x + m) = f(x)\) với mọi \(x\).
b. Lập bảng biến thiên của hàm số trên đoạn \([-1 ; 1]\).
c. Vẽ đồ thị của hàm số đó.
a. Đặt \(m = 2k, k \in\mathbb Z\). Ta có :
\(f(x + m) = \sinπ(x + m) = \sin(πx + 2kπ) = \sinπx = f(x)\)
b. Bảng biến thiên

c. Đồ thị
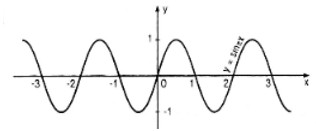
Câu 45. Đưa các biểu thức sau về dạng \(C\sin(x + α)\) :
a. \(\sin x + \tan {\pi \over 7}\cos x\)
b. \(\tan {\pi \over 7}\sin x + \cos x\)
a. Ta có:
Advertisements (Quảng cáo)
\(\eqalign{
& \sin x + \tan {\pi \over 7}\cos x = \sin x + {{\sin {\pi \over 7}} \over {\cos {\pi \over 7}}}\cos x \cr
& = {1 \over {\cos {\pi \over 7}}}\left( {\sin x\cos {\pi \over 7} + \sin {\pi \over 7}\cos x} \right) \cr
& = {1 \over {\cos {\pi \over 7}}}\sin \left( {x + {\pi \over 7}} \right) \cr} \)
b.
\(\eqalign{
& \tan {\pi \over 7}\sin x + \cos x = {{\sin {\pi \over 7}} \over {\cos {\pi \over 7}}}\sin x + \cos x \cr
& = {1 \over {\cos {\pi \over 7}}}\left( {\sin x\sin {\pi \over 7} + \cos x\cos {\pi \over 7}} \right) \cr
& = {1 \over {\cos {\pi \over 7}}}\cos \left( {x – {\pi \over 7}} \right) = {1 \over {\cos {\pi \over 7}}}\sin \left( {x – {\pi \over 7} + {\pi \over 2}} \right) \cr
& = {1 \over {\cos {\pi \over 7}}}\sin \left( {x + {{5\pi } \over {14}}} \right) \cr} \)
Câu 46. Giải các phương trình sau :
a. \(\sin \left( {x – {{2\pi } \over 3}} \right) = \cos 2x\)
b. \(\tan \left( {2x + 45^\circ } \right)\tan \left( {180^\circ – {x \over 2}} \right) = 1\)
c. \(\cos 2x – {\sin ^2}x = 0\)
d. \(5\tan x – 2\cot x = 3\)
a. Ta có:
\(\eqalign{& \sin \left( {x – {{2\pi } \over 3}} \right) = \cos 2x \cr & \Leftrightarrow \sin \left( {x – {{2\pi } \over 3}} \right) = \sin \left( {{\pi \over 2} – 2x} \right) \cr & \Leftrightarrow \left[ {\matrix{{x – {{2\pi } \over 3} = {\pi \over 2} – 2x + k2\pi } \cr {x – {{2\pi } \over 3} = \pi – {\pi \over 2} + 2x + k2\pi } \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{x = {{7\pi } \over {18}} + k{{2\pi } \over 3}} \cr {x = – {{7\pi } \over 6} – k2\pi } \cr} } \right. \cr} \)
b. Với ĐKXĐ của phương trình ta có \(\tan(2x + 45^0) = \cot(45^0 – 2x)\) và \(\tan \left( {180^\circ – {x \over 2}} \right) = \tan \left( { – {x \over 2}} \right)\) nên :
\(\eqalign{
& \tan \left( {2x + 45^\circ } \right)\tan \left( {180^\circ – {x \over 2}} \right) = 1 \cr
& \Leftrightarrow \cot \left( {45^\circ – 2x} \right)\tan \left( { – {x \over 2}} \right) = 1 \cr
& \Leftrightarrow \tan \left( { – {x \over 2}} \right) = \tan \left( {45^\circ – 2x} \right) \cr
& \Leftrightarrow – {x \over 2} = 45^\circ – 2x + k180^\circ \cr
& \Leftrightarrow x = 30^\circ + k120^\circ ,k \in\mathbb Z \cr} \)
c. Ta có:
\(\eqalign{
& \cos 2x – {\sin ^2}x = 0 \cr
& \Leftrightarrow \cos 2x – {{1 – \cos 2x} \over 2} = 0 \cr
& \Leftrightarrow 3\cos 2x – 1 = 0 \Leftrightarrow \cos 2x = {1 \over 3} \cr
& \Leftrightarrow \cos 2x = \cos \alpha \,\left( {\text{ với }\,\cos \alpha = {1 \over 3}} \right) \cr
& \Leftrightarrow x = \pm {\alpha \over 2} + k\pi \,\,(k\in\mathbb Z)\cr} \)
d.
\(\eqalign{& 5\tan x – 2\cot x = 3 \cr & \Leftrightarrow 5\tan x – {2 \over {\tan x}} = 3 \cr & \Leftrightarrow 3{\tan ^2}x – 3\tan x – 2 = 0 \cr & \Leftrightarrow \left[ {\matrix{{\tan x = 1} \cr {\tan x = – {2 \over 5}} \cr} } \right. \Leftrightarrow \left[ {\matrix{{x = {\pi \over 4} + k\pi } \cr {x = \alpha + k\pi } \cr}k\in\mathbb Z } \right. \cr & \text{trong đó}\,\tan \alpha = – {2 \over 5} \cr} \)
Câu 47. Giải các phương trình sau :
a. \(\sin 2x + {\sin ^2}x = {1 \over 2}\)
b. \(2{\sin ^2}x + 3\sin x\cos x + {\cos ^2}x = 0\)
c. \({\sin ^2}{x \over 2} + \sin x – 2{\cos ^2}{x \over 2} = {1 \over 2}\)
Advertisements (Quảng cáo)
Ta có:
\(\eqalign{
& \sin 2x + {\sin ^2}x = {1 \over 2} \cr
& \Leftrightarrow \sin 2x + {1 \over 2}\left( {1 – \cos 2x} \right) = {1 \over 2} \cr
& \Leftrightarrow \sin 2x – {1 \over 2}\cos 2x = 0 \cr
& \Leftrightarrow \tan 2x = {1 \over 2} \cr
& \Leftrightarrow 2x = \alpha + k\pi \,\text{ với }\,\tan \alpha = {1 \over 2} \cr
& \Leftrightarrow x = {\alpha \over 2} + k{\pi \over 2},\,k \in\mathbb Z \cr} \)
b.\(x = {\pi \over 2} + k\pi \) không là nghiệm phương trình.
Chia hai vế phương trình cho \({\cos ^2}x\) ta được :
\(\eqalign{& 2{\tan ^2}x + 3\tan x + 1 = 0 \Leftrightarrow \left[ {\matrix{{\tan x = – 1} \cr {\tan x = – {1 \over 2}} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{x = – {\pi \over 4} + k\pi } \cr {x = \alpha + k\pi } \cr} } \right.\,\left( {k \in\mathbb Z} \right) \cr & \left( {\text{ với }\,\tan \alpha = – {1 \over 2}} \right) \cr} \)
c. Ta có:
\(\eqalign{
& {\sin ^2}{x \over 2} + \sin x – 2{\cos ^2}{x \over 2} = {1 \over 2} \cr
& \Leftrightarrow {\sin ^2}{x \over 2} + 2\sin {x \over 2}\cos {x \over 2} – 2{\cos ^2}{x \over 2} = {1 \over 2} \cr} \)
Với \(x\) mà \(\cos {x \over 2} = 0\) không là nghiệm phương trình.
Chia hai vế phương trình cho \({\cos ^2}{x \over 2}\) ta được :
\(\eqalign{& {\tan ^2}{x \over 2} + 2\tan {x \over 2} – 2 = {1 \over 2}\left( {1 + {{\tan }^2}{x \over 2}} \right) \cr & \Leftrightarrow {\tan ^2}{x \over 2} + 4\tan {x \over 2} – 5 = 0 \cr & \Leftrightarrow \left[ {\matrix{{\tan {x \over 2} = 1} \cr {\tan {x \over 2} = – 5} \cr} } \right. \Leftrightarrow \left[ {\matrix{{{x \over 2} = {\pi \over 4} + k\pi } \cr {{x \over 2} = \alpha + k\pi } \cr} } \right.\,\left( {\text{ với }\,\tan \alpha = – 5} \right) \cr & \Leftrightarrow \left[ {\matrix{{x = {\pi \over 2} + k2\pi } \cr {x = 2\alpha + k2\pi } \cr} } \right.\,\left( {k \in\mathbb Z} \right) \cr} \)
Câu 48. a. Chứng minh rằng \(\sin {\pi \over {12}} = {{\sqrt 3 – 1} \over {2\sqrt 2 }}\)
b. Giải các phương trình \(2\sin x – 2\cos x =1 – \sqrt 3 \) bằng cách biến đổi vế trái về dạng \(C\sin(x + α)\).
c. Giải phương trình \(2\sin x – 2\cos x =1 – \sqrt 3 \) bằng cách bình phương hai vế.
a. Ta có:
\(\eqalign{
& \sin {\pi \over {12}} = \sin \left( {{\pi \over 3} – {\pi \over 4}} \right) \cr
& = \sin {\pi \over 3}\cos {\pi \over 4} – \sin {\pi \over 4}\cos {\pi \over 3} \cr
& = {{\sqrt 3 } \over 2}.{{\sqrt 2 } \over 2} – {{\sqrt 2 } \over 2}.{1 \over 2} \cr
& = {{\sqrt 6 – \sqrt 2 } \over 4} = {{\sqrt 2 \left( {\sqrt 3 – 1} \right)} \over 4} \cr
& = {{\sqrt 3 – 1} \over {2\sqrt 2 }} \cr} \)
b. Ta có:
\(\eqalign{& 2\sin x – 2\cos x = 1 – \sqrt 3 \cr & \Leftrightarrow {1 \over {\sqrt 2 }}\sin x – {1 \over {\sqrt 2 }}\cos x = {{1 – \sqrt 3 } \over {2\sqrt 2 }} \cr & \Leftrightarrow \sin x.\cos {\pi \over 4} – \sin {\pi \over 4}\cos x = – \sin {\pi \over {12}} \cr & \Leftrightarrow \sin \left( {x – {\pi \over 4}} \right) = \sin \left( { – {\pi \over {12}}} \right) \cr & \Leftrightarrow \left[ {\matrix{{x – {\pi \over 4} = – {\pi \over {12}} + k2\pi } \cr
{x – {\pi \over 4} = \pi + {\pi \over {12}} + k2\pi } \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{x = {\pi \over 6} + k2\pi } \cr {x = {{4\pi } \over 3} + k2\pi } \cr} } \right.\left( {k \in\mathbb Z} \right) \cr} \)
c. Chú ý rằng \(1 – \sqrt 3 < 0\), ta đặt điều kiện \(\sin x – \cos x < 0\) rồi bình phương hai vế của phương trình thì được :
\(\eqalign{& 4\left( {1 – \sin 2x} \right) = 4 – 2\sqrt 3 \cr & \Leftrightarrow \sin 2x = {{\sqrt 3 } \over 2} \Leftrightarrow \left[ {\matrix{{x = {\pi \over 6} + k\pi } \cr {x = {\pi \over 3} + k\pi } \cr}\,\,(k\in\mathbb Z) } \right. \cr} \)
Thử vào điều kiện \(\sin x – \cos x < 0\), ta thấy :
* Họ nghiệm \(x = {\pi \over 6} + k\pi \) thỏa mãn điều kiện \(\sin x – \cos x < 0\) khi và chỉ khi \(k\) chẵn, tức là \(x = {\pi \over 6} + 2m\pi \) với \(m \in\mathbb Z\).
* Họ nghiệm \(x = {\pi \over 3} + k\pi \) thỏa mãn điều kiện \(\sin x – \cos x < 0\) khi và chỉ khi \(k\) lẻ, tức là \(x = {\pi \over 3} + \left( {2m + 1} \right)\pi = {{4\pi } \over 3} + 2m\pi \) với \(m \in\mathbb Z\).
Ta có kết quả như đã nêu ở câu b.
Câu 49. Giải phương trình :
\({{1 + \cos 2x} \over {\cos x}} = {{\sin 2x} \over {1 – \cos 2x}}\)
ĐKXĐ :\(\cos x \ne 0\,\text{ và }\,\cos 2x \ne 1.\) Với điều kiện đó, ta có:
\(\eqalign{& {{1 + \cos 2x} \over {\cos x}} = {{\sin 2x} \over {1 – \cos 2x}} \cr & \Leftrightarrow {{2{{\cos }^2}x} \over {\cos x}} = {{2\sin x\cos x} \over {2{{\sin }^2}x}} \cr & \Leftrightarrow 1 – {1 \over {2\sin x}} = 0 \cr & \Leftrightarrow \sin x = {1 \over 2} \Leftrightarrow \left[ {\matrix{{x = {\pi \over 6} + k2\pi \,\left( \text{nhận} \right)} \cr {x = {{5\pi } \over 6} + k2\pi \,\left( \text{nhận} \right)} \cr} } \right. \cr} \)
Câu 50. Cho phương trình \({{{{\sin }^3}x + {{\cos }^3}x} \over {2\cos x – \sin x}} = \cos 2x.\)
a. Chứng minh rằng \(x = {\pi \over 2} + k\pi \) nghiệm đúng phương trình.
b. Giải phương trình bằng cách đặt \(\tan x = t\) (khi \(x \ne {\pi \over 2} + k\pi \) )
a. Thay \(x = {\pi \over 2} + k\pi \) vào phương trình ta được :
\({{{{\left( { – 1} \right)}^{3k}}} \over { – {{\left( { – 1} \right)}^k}}} = \cos \pi \Leftrightarrow – 1 = – 1\) (luôn đúng)
Vậy \(x = {\pi \over 2} + k\pi \) là nghiệm phương trình
b. * \(x = {\pi \over 2} + k\pi \) là nghiệm phương trình.
* Với \(x \ne {\pi \over 2} + k\pi \) chia tử và mẫu của vế trái cho \({\cos ^3}x\) ta được :
\({{{{\tan }^3}x + 1} \over {2\left( {1 + {{\tan }^2}x} \right) – \tan x\left( {1 + {{\tan }^2}x} \right)}} = {{1 – {{\tan }^2}x} \over {1 + {{\tan }^2}x}}\)
Đặt \(t = \tan x\) ta được :
\(\eqalign{& {{{t^3} + 1} \over {\left( {2 – t} \right)\left( {1 + {t^2}} \right)}} = {{1 – {t^2}} \over {1 + {t^2}}} \cr & \Leftrightarrow {t^3} + 1 = \left( {{t^2} – 1} \right)\left( {t – 2} \right) \cr & \Leftrightarrow {t^3} + 1 = {t^3} – 2{t^2} – t + 2 \cr & \Leftrightarrow 2{t^2} + t – 1 = 0 \Leftrightarrow \left[ {\matrix{
{t = – 1} \cr {t = {1 \over 2}} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{\tan x = – 1} \cr {\tan x = {1 \over 2}} \cr} } \right. \Leftrightarrow \left[ {\matrix{{x = – {\pi \over 4} + k\pi } \cr {x = \alpha + k\pi } \cr} } \right. \cr & \text{ với }\,\tan \alpha = {1 \over 2} \cr} \)
Vậy phương trình đã cho có nghiệm :\(x = {\pi \over 2} + k\pi ,x = – {\pi \over 4} + k\pi ,x = \alpha + k\pi \,\left( {k \in\mathbb Z} \right)\)

