Bài 34-35 Chất rắn kết tinh, chất rắn vô định dạng, biến dạng cơ của vật rắn SBT Lý lớp 10. Giải bài 34-35.9, 34-35.10, 34-35.11, 34-35.12 trang 84 Sách bài tập Vật lí 10. Câu 34-35.9: Một chiếc cột bê tông cốt thép chịu lực nén F thẳng đứng do tải trọng đè lên nó…
Bài 34 – 35.9: Một chiếc cột bê tông cốt thép chịu lực nén F thẳng đứng do tải trọng đè lên nó. Giả sử suất đàn hồi của bê tông bằng 1/10 của thép, còn diện tích tiết diện ngang của thép bằng khoảng 1/20 của bê tông. Hãy tính phần lực nén do tải trọng tác dụng lên phần bê tông của chiếc cột này.
Gọi F1 là phần lực nén do tải trọng tác dụng lên phần bê tông của chiếc cột và F2 là phần lực nén do tải trọng tác dụng lên phần cốt thép của chiếc cột. Áp dụng định luật Húc, ta có :
\({F_1} = {E_1}{{{S_1}} \over l}\Delta l\) và \({F_2} = {E_2}{{{S_2}} \over l}\Delta l\)
So sánh F1 với F2 , với chú ý E1/E2 = 1/10 và S2/S1 = 1/20, ta tìm được
\({{{F_1}} \over {{F_2}}} = {{{E_1}{S_1}} \over {{E_2}{S_2}}} = 2\)
Vì F1 + F2 = F, nên ta suy ra : F1 = 2/3 F
Như vậy, lực nén lên bê tông bằng 2/3 lực nén của tải trọng tác dụng lên cột.
Bài 34 – 35.10: Một chiếc vòng đồng bán kính 100 cm và tiết diện 4 mm2 được lồng khít vào mặt ngoài của một thanh thép bán kính 100,05 cm. Tính lực tác dụng tối thiểu đủ để làm găng (dãn) chiếc vòng đồng, nếu suất đàn hồi của đồ là E ≈ 12.1010Pa. Bỏ qụa biến dạng của thanh thép.
Gọi r là bán kính của vòng đồng và R là bán kính của thanh thép. Sau khi được lồng vào thanh thép, chiếc vòng đồng bị dãn dài thêm một đoạn :
Δl = 2πR – 2πr = 2π(R – r)
Theo định luật Húc, lực cần tác dụng để làm dãn chiếc vòng đồng bằng :
\(F = E{S \over {{l_0}}}\Delta l = E{S \over {2\pi r}}2\pi \left( {R – r} \right) = E{{S\left( {R – r} \right)} \over r}\)
Thay số ta tìm được :
Advertisements (Quảng cáo)
\(F = {12.10^{10}}{{{{4.10}^{ – 6}}\left( {100,05 – 100} \right)} \over {100}} = 240\left( N \right)\)
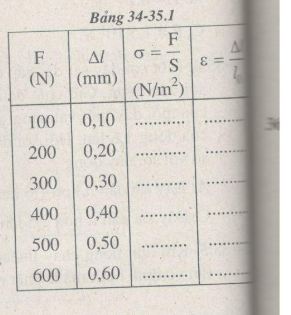
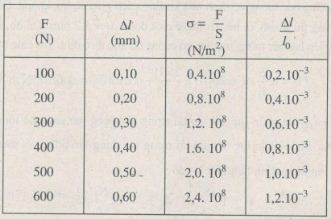
Bài 34 – 35.11*: Người ta dùng một thanh sắt tròn có độ dài ban đầu l0= 50 cm và tiết diện ngang S = 2,5 mm2. Kéo dãn thanh sắt bằng lực F có cường độ tăng dần và đo độ dãn dài Δl tương ứng của nó (Bảng 34-35. 1).
a) Tính độ dãn dài tỉ đối ε của thanh sắt và ứng suất σ của lực kéo tác dụng lên nó trong mỗi lần đo (Bảng 34-35. 1).
b) Vẽ đồ thị biểu diễn sự phụ thuộc của ε vào ε.
c) Dựa vào đồ thị vẽ được, tìm giá trị của suất đàn hồi E và hệ số đàn hồi k.
a) Tính độ dãn dài tỉ đối ε của thanh sắt và ứng suất σ của lực kéo tác dụng lên thanh sắt trong mỗi lần đo.
b) Vẽ đồ thị biểu diễn sự phụ thuộc của ε vào σ.
Advertisements (Quảng cáo)
Chọn tỉ lệ vẽ trên các trục tọa độ:
– Trục hoành: 1 cm → σ = 0,5.108 N/m2.
– Trục tung: 1 cm → ε = 0,2.10-3.
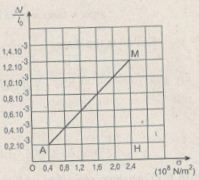
Đồ thị có dạng đường thẳng chứng tỏ độ biến dạng tỉ đối Δl/l0 của thanh sắt tỉ lệ thuận với ứng suất σ của lực kéo tác dụng lên thanh sắt, nghĩa là:
\(\varepsilon = {{\Delta l} \over {{l_0}}} = a\varepsilon \)
Hệ số tỉ lệ a được xác định bởi hệ số góc của đường biểu diễn đồ thị:
\(\tan \theta = {{MH} \over {AH}} = {{1,{{2.10}^{ – 3}} – 0,{{2.10}^{ – 3}}} \over {2,{{4.10}^8} – 0,{{4.10}^8}}} = 0,{5.10^{ – 11}}\)
c) Tìm giá trị của suất đàn hồi E và hệ số đàn hồi k của thanh sắt.
Theo định luật Húc :\(F = k\left| {\Delta l} \right| = E{S \over {{l_0}}}\Delta l\) , ta suy ra \({{\Delta l} \over {{l_0}}} = {1 \over E}.{F \over S}\)
Từ đó tìm đươc suất đàn hồi : \(E = {1 \over {\tan \theta }} = {1 \over {0,{{5.10}^{ – 11}}}} = {20.10^{10}}Pa\)
và hệ số đàn hồi: \(k = E{S \over {{l_0}}} = {20.10^{10}}.{{2,{{5.10}^{ – 6}}} \over {{{50.10}^{ – 2}}}} = {1.10^6}N/m\
Bài 34 – 35.12*: Một sợi dày thép tiết diện S = 5,0 mm2 căng ngang giữa hai đỉnh cột A, B. Tại trung điểm H của sợi dây, người ta treo một hộp đèn chiếu sáng trọng lượng P = 50 N, làm cho sợi dây trùng xuống tới vị trí AMB hợp với phương ban đầu một góc lệch nhỏ α (Hình 34-35.1). Tính góc α, cho biết suất đàn hồi của thép là E = 20.1010 Pa.
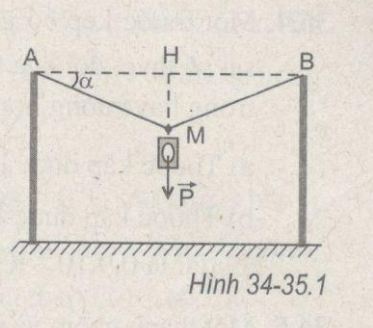
Lực căng của sợi dây thép : \(T = {P \over {2\sin \alpha }}\)
Mặt khác theo định luật Húc : \($T = E{S \over l}\Delta l\)
Vì độ biến dạng Δl của sợi dây thép bằng :
\(\Delta l = 2\left( {AM – AH} \right) = 2\left( {{1 \over {2\cos \alpha }} – {1 \over 2}} \right) = {{1.\left( {1 – \cos \alpha } \right)} \over {\cos \alpha }}\)
nên : \(T = {\rm{ES}}{{1 – \cos \alpha } \over {\cos \alpha }}\)
Với α nhỏ, có thể coi gần đúng :
\(\sin \alpha \approx \tan \alpha {\rm{ }} \approx {\rm{ }}\alpha ;cos\alpha = 1 – 2{\sin ^2}\left( {{\alpha \over 2}} \right) \approx 1 – {{{\alpha ^2}} \over 2}\)
Khi đó ta tìm được :
\(\alpha = \root 3 \of {{P \over {ES}}} = \root 3 \of {{{50} \over {{{20.10}^{10}}{{.5.10}^{ – 6}}}}} = 2,{154.10^{ – 2}} \approx 0,022\left( {rad} \right)\)

