Câu 1. a. Tính \(\sin {\pi \over 8}\,\text{ và }\,\cos {\pi \over 8}\)
b. Chứng minh rằng có hằng số C > 0 để có đẳng thức
\(\sin x + \left( {\sqrt 2 – 1} \right)\cos x = C\cos \left( {x – {{3\pi } \over 8}} \right)\) với mọi x.
a. Ta có:
\(\eqalign{ & {\sin ^2}{\pi \over 8} = {{1 – \cos {\pi \over 4}} \over 2} = {{1 – {{\sqrt 2 } \over 2}} \over 2} = {{2 – \sqrt 2 } \over 4} \cr & \Rightarrow \sin {\pi \over 8} = {1 \over 2}\sqrt {2 – \sqrt 2 } \cr & {\cos ^2}{\pi \over 8} = {{1 + \cos {\pi \over 4}} \over 2} = {{1 + {{\sqrt 2 } \over 2}} \over 2} = {{2 + \sqrt 2 } \over 4} \cr & \Rightarrow \cos {\pi \over 8} = {1 \over 2}\sqrt {2 + \sqrt 2 } \cr} \)
b. Ta có:
\(\eqalign{ & {1^2} + {\left( {\sqrt 2 – 1} \right)^2} = 4 – 2\sqrt 2 .\,\text{ Do đó}\,: \cr & \sin x + \left( {\sqrt 2 – 1} \right)\cos x \cr & = \left( {\sqrt {4 – 2\sqrt 2 } } \right)\left( {{1 \over {\sqrt {4 – 2\sqrt 2 } }}\sin x + {{\sqrt 2 – 1} \over {\sqrt {4 – 2\sqrt 2 } }}\cos x} \right) \cr & = \sqrt {4 – 2\sqrt 2 } \left( {\sin x\cos {\pi \over 8} + \sin {\pi \over 8}\cos x} \right) \cr & = \sqrt {4 – 2\sqrt 2 } \sin \left( {x + {\pi \over 8}} \right) \cr & = \sqrt {4 – 2\sqrt 2 } \cos \left( {x – {{3\pi } \over 8}} \right) \cr & \text{ Vì }\,{1 \over {\sqrt {4 – 2\sqrt 2 } }} = {{\sqrt {4 + 2\sqrt 2 } } \over {\sqrt 8 }} = {1 \over 2}\sqrt {2 + \sqrt 2 } = \cos {\pi \over 8}. \cr & \text{Vậy }\,C = \sqrt {4 – 2\sqrt 2 } \cr} \)
Câu 2. Giải phương trình
\(\tan x = \cot 2x\)
Biểu diễn các nghiệm trên đường tròn lượng giác.
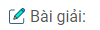
Điều kiện
\({\mathop{\rm cosx}\nolimits} .sin2x \ne 0 \Leftrightarrow \left\{ {\matrix{ {\sin x \ne 0} \cr {\cos x \ne 0} \cr } } \right. \Leftrightarrow x \ne k{\pi \over 2}\)
\(\eqalign{ & \tan x = \cot 2x \Leftrightarrow {{\sin x} \over {\cos x}} = {{\cos 2x} \over {\sin 2x}} \cr& \Leftrightarrow\cos x \cos 2x – \sin x\sin 2x = 0 \cr & \Leftrightarrow \cos 3x = 0 \Leftrightarrow \cos x\left( {4{{\cos }^2}x – 3} \right) = 0 \cr & \Leftrightarrow {\cos ^2}x = {3 \over 4} \cr & \Leftrightarrow {{1 + \cos 2x} \over 2} = {3 \over 4} \Leftrightarrow \cos 2x = {1 \over 2} \cr & \Leftrightarrow x =\pm {\pi \over 6} + k\pi (k\in\mathbb Z) \cr} \)
Biểu diễn nghiệm trên đường tròn được 4 điểm.
Câu 3. a. Tìm giá trị nhỏ nhất của biểu thức \(P\left( x \right) = {\left( {\sin x + \cos x} \right)^3}\)
b. Tìm giá trị nhỏ nhất của biểu thức \(Q\left( x \right) = {1 \over {{{\sin }^2}x{{\cos }^2}x}}\)
c. Tìm giá trị nhỏ nhất của biểu thức \(R\left( x \right) = P\left( x \right) + Q\left( x \right)\)
Advertisements (Quảng cáo)
a. \(P\left( x \right) = 2\sqrt 2 {\cos ^3}\left( {x – {\pi \over 4}} \right) \ge – 2\sqrt 2 \) (đẳng thức xảy ra khi \(x = – {{3\pi } \over 4}+k2\pi\) )
Vậy \(\min P\left( x \right) = – 2\sqrt 2 \)
b. \(Q\left( x \right) = {4 \over {{{\sin }^2}2x}} \ge 4\) (đẳng thức xảy ra, chẳng hạn khi \(x = \pm {{3\pi } \over 4}\) )
Vậy min Q(x) = 4
c. \(R\left( x \right) = P\left( x \right) + Q\left( x \right) \ge 4 – 2\sqrt 2 \) (đẳng thức xảy ra, chẳng hạn khi \(x = – {{3\pi } \over 4}\)
Vậy \({\mathop{\rm min\,R}\nolimits} \left( x \right) = 4 – 2\sqrt 2 \)
Câu 4. Giải các phương trình :
a. \({\sin ^4}x + {\cos ^4}x = {3 \over 4}\)
b. \({\sin ^2}2x – {\sin ^2}x = {\sin ^2}{\pi \over 4}\)
c. \(\cos x\cos 2x = \cos 3x\)
d. \(\tan 2x – \sin 2x + \cos 2x – 1 = 0\)
Advertisements (Quảng cáo)
a.
\(\eqalign{ & {\sin ^4}x + {\cos ^4}x = {3 \over 4} \cr & \Leftrightarrow 1 – 2{\sin ^2}x{\cos ^2}x = {3 \over 4} \cr & \Leftrightarrow 1 – {1 \over 2}{\sin ^2}2x = {3 \over 4} \cr & \Leftrightarrow {\sin ^2}2x = {1 \over 2} \Leftrightarrow {{1 – \cos 4x} \over 2} = {1 \over 2} \cr & \Leftrightarrow \cos 4x = 0 \Leftrightarrow x = {\pi \over 8} + k{\pi \over 4},k \in\mathbb Z \cr} \)
b.
\(\eqalign{ & {\sin ^2}2x – {\sin ^2}x = {\sin ^2}{\pi \over 4} \cr & \Leftrightarrow 4{\sin ^2}x{\cos ^2}x – {\sin ^2}x = {1 \over 2} \cr & \Leftrightarrow 8{\sin ^2}x\left( {1 – {{\sin }^2}x} \right) – 2{\sin ^2}x = 1 \cr & \Leftrightarrow 8{\sin ^4}x – 6{\sin ^2}x + 1 = 0 \cr & \Leftrightarrow \left[ {\matrix{ {{{\sin }^2}x = {1 \over 2}} \cr {{{\sin }^2}x = {1 \over 4}} \cr } } \right. \Leftrightarrow \left[ {\matrix{ {{{1 – \cos 2x} \over 2} = {1 \over 2}} \cr {{{1 – \cos 2x} \over 2} = {1 \over 4}} \cr } } \right. \cr & \Leftrightarrow \left[ {\matrix{ {\cos 2x = 0} \cr {\cos 2x = {1 \over 2}} \cr } } \right. \Leftrightarrow \left[ {\matrix{ {x = {\pi \over 4} + k{\pi \over 2}} \cr {x = {\pi \over 6} + k{\pi \over 2}} \cr } } \right. \cr} \)
c.
\(\eqalign{ & \cos x\cos 2x = \cos 3x \cr & \Leftrightarrow {1 \over 2}\left( {\cos 3x + \cos x} \right) = \cos 3x \cr & \Leftrightarrow \cos 3x = \cos x \cr & \Leftrightarrow \left[ {\matrix{ {3x = x + k2\pi } \cr {3x = – x + k2\pi } \cr } } \right. \Leftrightarrow \left[ {\matrix{ {x = k\pi } \cr {x = k{\pi \over 2}} \cr } } \right.\cr& \Leftrightarrow x = k{\pi \over 2},k \in\mathbb Z \cr} \)
d. Điều kiên: \(\cos 2x \ne0\)
\(\eqalign{ & \tan 2x – \sin 2x + \cos 2x – 1 = 0 \cr & \Leftrightarrow \tan 2x\left( {1 – \cos 2x} \right) – \left( {1 – \cos 2x} \right) = 0 \cr & \Leftrightarrow \left( {1 – \cos 2x} \right)\left( {\tan 2x – 1} \right) = 0 \cr & \Leftrightarrow \left[ {\matrix{ {\tan 2x = 1} \cr {\cos 2x = 1} \cr } } \right. \Leftrightarrow \left[ {\matrix{ {x = {\pi \over 8} + k{\pi \over 2}} \cr {x = k\pi } \cr } } \right. k \in\mathbb Z \cr} \)
Câu 5. Giải các phương trình sau :
a. \(2\sin \left( {x + 10^\circ } \right) – \sqrt {12} \cos \left( {x + 10^\circ } \right) = 3\)
b. \(\sqrt 3 \cos 5x + \sin 5x = 2\cos 3x\)
c. \({\sin ^2}x – 3\sin x\cos x + 2{\cos ^2}x = 0\)
a.
\({a^2} + {b^2} = {2^2} + {\left( { – \sqrt {12} } \right)^2} = 16.\) Chia hai vế cho \(\sqrt {{a^2} + {b^2}} = 4\) ta được :
\(\eqalign{ & {1 \over 2}\sin \left( {x + 10^\circ } \right) – {{\sqrt 3 } \over 2}\cos \left( {x + 10^\circ } \right) = {3 \over 4} \cr & \Leftrightarrow \sin \left( {x + 10^\circ } \right)\cos 60^\circ – \sin 60^\circ \cos \left( {x + 10^\circ } \right) = {3 \over 4} \cr & \Leftrightarrow \sin \left( {x – 50^\circ } \right) = \sin \alpha \,\text{ với }\,\sin \alpha = {3 \over 4} \cr & \Leftrightarrow \left[ {\matrix{ {x – 50^\circ = \alpha + k360^\circ } \cr {x – 50^\circ = 180^\circ – \alpha + k360^\circ } \cr } } \right. \cr & \Leftrightarrow \left[ {\matrix{ {x = \alpha + 50^\circ + k360^\circ } \cr {x = 230^\circ – \alpha + k360^\circ } \cr } } \right. \cr} \)
b.
\(\eqalign{ & \sqrt 3 \cos 5x + \sin 5x = 2\cos 3x \cr & \Leftrightarrow {{\sqrt 3 } \over 2}\cos 5x + {1 \over 2}\sin 5x = \cos 3x \cr & \Leftrightarrow \cos 5x.\cos {\pi \over 6} + \sin 5x\sin {\pi \over 6} = \cos 3x \cr & \Leftrightarrow \cos \left( {5x – {\pi \over 6}} \right) = \cos 3x \cr & \Leftrightarrow \left[ {\matrix{ {5x – {\pi \over 6} = 3x + k2\pi } \cr {5x – {\pi \over 6} = – 3x + k2\pi } \cr } } \right. \Leftrightarrow \left[ {\matrix{ {x = {\pi \over {12}} + k\pi } \cr {x = {\pi \over {48}} + k{\pi \over 4}} \cr } } \right. \cr} \)
c. * \(\cos x = 0 \Rightarrow \sin x = \pm 1\,\text{ nên }\,x = {\pi \over 2} + k\pi \) không là nghiệm của phương trình.
* Chia hai vế phương trình cho \({\cos ^2}x\) ta được :
\({\tan ^2}x – 3\tan x + 2 = 0 \Leftrightarrow \left[ {\matrix{ {\tan x = 1} \cr {\tan x = 2} \cr } } \right.\)
\(\Leftrightarrow \left[ {\matrix{ {x = {\pi \over 4} + k\pi } \cr {x = \arctan 2 + k\pi } \cr } } \right.\)

