Câu 1. Ba vecto \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) có đồng phẳng không nếu một trong hai điều sau đây xảy ra ?
a. Có một vecto trong ba vecto đó bằng \(\overrightarrow 0 \)
b. Có hai vecto trong ba vecto đó cùng phương.
a. Giả sử \(\overrightarrow a = \overrightarrow 0 .\) Áp dụng định lí 1 : \(\overrightarrow a = 0.\overrightarrow b + 0.\overrightarrow c \) nên \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng.
b. Giả sử \(\overrightarrow a ,\overrightarrow b \) cùng phương, khi đó có số k sao cho \(\overrightarrow a = k\overrightarrow b \)
\( \Rightarrow \overrightarrow a = k\overrightarrow b + 0.\overrightarrow c \) do đó \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng.
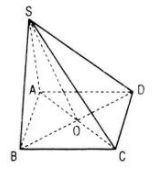
Câu 2. Cho hình chóp S.ABCD.
a. Chứng minh rằng nếu ABCD là hình bình hành thì \(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \). Điều ngược lại có đúng không ?
b. Gọi O là giao điểm của AC và BD. Chứng tỏ rằng ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \)
a. Ta có:
\(\eqalign{ & \overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \cr & \Leftrightarrow \overrightarrow {SB} – \overrightarrow {SC} = \overrightarrow {SA} – \overrightarrow {SD} \Leftrightarrow \overrightarrow {CB} = \overrightarrow {DA} \cr} \)
⇔ ABCD là hình bình hành.
b. Ta có:
\(\eqalign{ & \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \cr & \Leftrightarrow \overrightarrow {SO} + \overrightarrow {OA} + \overrightarrow {SO} + \overrightarrow {OB} + \overrightarrow {SO} + \overrightarrow {OC} + \overrightarrow {SO} + \overrightarrow {OD} = 4\overrightarrow {SO} \cr & \Leftrightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \,\,\left( * \right) \cr} \)
Nếu ABCD là hình bình hành thì \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \) suy ra
\(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \) (do (*))
Ngược lại, giả sử \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} ,\) ta có (*).
Gọi M, N lần lượt là trung điểm của AC, BD thì :
Advertisements (Quảng cáo)
\(\overrightarrow {OA} + \overrightarrow {OC} = 2\overrightarrow {OM} ,\overrightarrow {OB} + \overrightarrow {OD} = 2\overrightarrow {ON} \)
Từ (*) suy ra \(2\left( {\overrightarrow {OM} + \overrightarrow {ON} } \right) = \overrightarrow 0 ,\) điều này chứng tỏ O, M, N thẳng hàng
Mặt khác, M thuộc AC, N thuộc BD và O là giao điểm của AC và BD nên O, M, N thẳng hàng chỉ xảy ra khi O ≡ M ≡ N, tức O là trung điểm AC và BD, hay ABCD là hình bình hành.
Câu 3. Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi G và G’ lần lượt là trọng tâm của tam giác ABC và A’B’C’, I là giao điểm của hai đường thẳng AB’ và A’B. Chứng minh rằng các đường thẳng GI và CG’ song song với nhau.
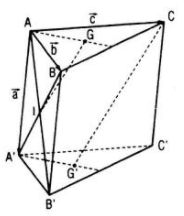
Đặt \(\overrightarrow {AA’} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow c \)
Thì \(\overrightarrow {AG} = {1 \over 3}\left( {\overrightarrow b + \overrightarrow c } \right),\overrightarrow {AI} = {1 \over 2}\left( {\overrightarrow a + \overrightarrow b } \right)\)
Do đó, \(\overrightarrow {GI} = \overrightarrow {AI} – \overrightarrow {AG} = {{3\overrightarrow a + \overrightarrow b – 2\overrightarrow c } \over 6}\)
Mặt khác : \(\overrightarrow {AG’} = {1 \over 3}\left( {\overrightarrow {AA’} + \overrightarrow {AB’} + \overrightarrow {AC’} } \right) = \overrightarrow a + {1 \over 3}\left( {\overrightarrow b + \overrightarrow c } \right)\)
\( \Rightarrow \overrightarrow {CG’} = \overrightarrow {AG’} – \overrightarrow {AC} = \overrightarrow a + {1 \over 3}\left( {\overrightarrow b + \overrightarrow c } \right) – \overrightarrow c \)
\(= {{3\overrightarrow a + \overrightarrow b – 2\overrightarrow c } \over 3}\)
Vậy \(\overrightarrow {CG’} = 2\overrightarrow {GI} .\) Ngoài ra, điểm G không thuộc đường thẳng CG’ nên GI và CG’ là hai đường thẳng song song.
Advertisements (Quảng cáo)
Câu 4. Cho hình hộp ABCD.A’B’C’D’. Gọi M và N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của các tứ diện A’D’MN và BCC’D’. Chứng minh rằng đường thẳng GG’ và mặt phẳng (ABB’A’) song song với nhau.
Giải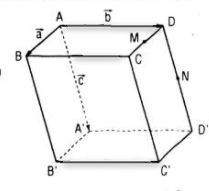
Đặt \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AD} = \overrightarrow b ,\overrightarrow {AA’} = \overrightarrow c .\)
Vì G’ là trọng tâm tứ diện BCC’D’ nên \(\overrightarrow {AG’} = {1 \over 4}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AC’} + \overrightarrow {AD’} } \right)\)
Và G là trọng tâm tứ diện A’D’MN nên
\(\eqalign{ & \overrightarrow {AG} = {1 \over 4}\left( {\overrightarrow {AA’} + \overrightarrow {AD’} + \overrightarrow {AM} + \overrightarrow {AN} } \right) \cr & \Rightarrow \overrightarrow {GG’} = \overrightarrow {AG’} – \overrightarrow {AG} \cr& = {1 \over 4}\left( {\overrightarrow {A’B} + \overrightarrow {D’C} + \overrightarrow {MC’} + \overrightarrow {ND’} } \right) \cr & = {1 \over 4}\left( {\overrightarrow a – \overrightarrow c + \overrightarrow a – \overrightarrow c + {1 \over 2}\overrightarrow a + \overrightarrow c + {1 \over 2}\overrightarrow c } \right) \cr & = {1 \over 8}\left( {5\overrightarrow a – \overrightarrow c } \right) = {1 \over 8}\left( {5\overrightarrow {AB} – \overrightarrow {AA’} } \right) \cr} \)
Do đó \(\overrightarrow {AB} ,\overrightarrow {AA’} ,\overrightarrow {GG’} \) đồng phẳng. Mặt khác, G không thuộc mặt phẳng (ABB’A’) nên đường thẳng GG’ và mặt phẳng (ABB’A’) song song với nhau.
Câu 5. Trong không gian cho tam giác ABC.
a. Chứng minh rằng nếu điểm M thuộc mp(ABC) thì có ba số x, y, z mà x + y + z = 1 sao cho \(\overrightarrow {OM} = \overrightarrow {xOA} + \overrightarrow {yOB} + \overrightarrow {zOC} \) với mọi điểm O.
b. Ngược lại, nếu có một điểm O trong không gian saao cho \(\overrightarrow {OM} = \overrightarrow {xOA} + \overrightarrow {yOB} + \overrightarrow {zOC} ,\) trong đó x + y + z = 1 thì điểm M thuộc mp(ABC).
a. Vì \(\overrightarrow {AB} ,\overrightarrow {AC} \) là hai vecto không cùng phương nên điểm M thuộc mp(ABC) khi và chỉ khi có \(\overrightarrow {AM} = l\overrightarrow {AB} + m\overrightarrow {AC} \)
hay \(\overrightarrow {OM} – \overrightarrow {OA} = l\left( {\overrightarrow {OB} – \overrightarrow {OA} } \right) + m\left( {\overrightarrow {OC} – \overrightarrow {OA} } \right)\) với mọi điểm O
tức là \(\overrightarrow {OM} = \left( {1 – l – m} \right)\overrightarrow {OA} + l\overrightarrow {OB} + m\overrightarrow {OC} \)
đặt \(1 – l – m = x,l = y,m = z\) thì \(\overrightarrow {OM} = x\overrightarrow {OA} + y\overrightarrow {OB} + z\overrightarrow {OC} \) với \(x + y + z = 1.\)
b. Giả sử \(\overrightarrow {OM} = x\overrightarrow {OA} + y\overrightarrow {OB} + z\overrightarrow {OC} \) với \(x + y + z = 1,\) ta có :
\(\eqalign{ & \overrightarrow {OM} = \left( {1 – y – z} \right)\overrightarrow {OA} + y\overrightarrow {OB} + z\overrightarrow {OC} \cr & hay\,\overrightarrow {OM} – \overrightarrow {OA} = y\overrightarrow {AB} + z\overrightarrow {AC} \cr & \text{ tức là }\overrightarrow {AM} = y\overrightarrow {AB} + z\overrightarrow {AC} \cr} \)
Mà \(\overrightarrow {AB} ,\overrightarrow {AC} \) không cùng phương nên M thuộc mặt phẳng (ABC)
Câu 6. Cho hình chóp S.ABC. Lấy các điểm A’, B’, C’ lần lượt thuộc các tia SA, SB, SC sao cho SA = aSA’, SB = bSB’, SC = cSC’, trong đó a, b, c là các số thay đổi. Chứng minh rằng mặt phẳng (A’B’C’) đi qua trọng tâm của tam giác ABC khi và chỉ khi a + b + c = 3.
Ta có: \(\overrightarrow {SA} = a\overrightarrow {SA’} ,\;\overrightarrow {SB} = b\overrightarrow {SB’} ,\;\overrightarrow {SC} = c\overrightarrow {SC} .\)
Gọi G là trọng tâm của tam giác ABC thì
\(\eqalign{ & \overrightarrow {SG} = {1 \over 3}.\left( {\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} } \right) \cr & Vay\,\overrightarrow {SG} = {a \over 3}\overrightarrow {SA’} + {b \over 3}\overrightarrow {SB’} + {c \over 3}\overrightarrow {SC’} \cr} \)
Mặt phẳng (A’B’C’) đi qua G khi và chỉ khi 4 điểm G, A’, B’, C’ đồng phẳng, nên theo kết quả bài tập 5 (SGK trang 91) , điều đó xảy ra nếu và chỉ nếu \({a \over 3} + {b \over 3} + {c \over 3} = 1\) , tức là: a + b + c = 3.

