Câu 25. Các phép sau đây có phải là phép vị tự hay không: phép đối xứng tâm, phép đối xứng trục, phép đồng nhất, phép tịnh tiến theo vectơ khác \(\vec 0\)?
Giải
Phép đối xứng tâm qua O là phép vị tự tâm O tỉ số -1
Phép đối xứng trục không phải là phép vị tự vì các đường thẳng nối cặp điểm tương ứng không đồng quy
Phép đồng nhất là phép vị tự với tâm là điểm bất kì và tỉ số \(k = 1\)
Phép tịnh tiến theo vecto khác \(\vec 0\) không phải là phép vị tự vì không có điểm nào biến thành chính nó
Câu 26. Các khẳng định sau đây có đúng không ?
a. Phép vị tự luôn có điểm bất động (tức là điểm biến thành chính nó)
b. Phép vị tự không thể có quá một điểm bất động
c. Nếu phép vị tự có hai điểm bất động phân biệt thì mọi điểm đều bất động
Giải
a. Đúng. Tâm vị tự là điểm bất động
b. Sai. Phép vị tự tỉ số \(k = 1\) có mọi điểm đều là bất động
c. Đúng. Phép vị tự tâm O luôn có điểm bất động O, nếu nó còn điểm bất động nữa là M (tức là ảnh M’ của M trùng với M) thì vì \(\overrightarrow {OM} = \overrightarrow {OM’} = k\overrightarrow {OM} \) nên \(k = 1\)
Vậy phép vị tự đó là phép đồng nhất nên mọi điểm đều bất động
Câu 27. Xác định tâm vị tự trong và tâm vị tự ngoài của hai đường tròn trong các trường hợp sau :
a. Hai đường tròn tiếp xúc ngoài với nhau
b. Hai đường tròn tiếp xúc trong với nhau
c. Một đường tròn chứa đường tròn kia
Giải
Advertisements (Quảng cáo)
Gọi I là tâm vị tự ngoài, I’ là tâm vị tự trong của hia đường tròn \((O)\) và \((O’)\)
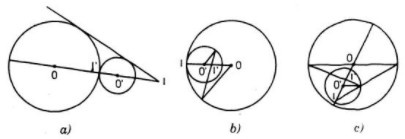
a. Nếu \((O)\) và \((O’)\) tiếp xúc ngoài thì tiếp điểm I’ là tâm vị tự trong, giao điểm của OO’ với tiếp tuyến chung ngoài của \((O)\) và \((O’)\) (nếu có) là tâm vị tự ngoài (h.a)
b. Nếu \((O)\) và \((O’)\) tiếp xúc trong thì tiếp điểm I là tâm vị tự ngoài, tâm vị tự trong I’ xác định như hình vẽ b)
c. Nếu \((O)\) chứa \((O’)\) thì xác định I và I’ như hình vẽ c) ( đặc biệt, khi O trùng O’ thì I và I’ trùng O)
Câu 28. Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Hãy dựng qua A một đường thẳng d cắt (O) ở M và (O)’ ở N sao cho M là trung điểm của AN
Giải
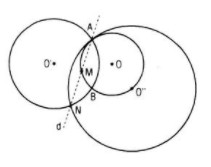
Giả sử đã dựng được đường thẳng d theo yêu cầu của bài toán.
Vì M là trung điểm AN nên \(\overrightarrow {AN} = 2\overrightarrow {AM} \)
Như vậy, gọi V là phép vị tự tâm A tỉ số 2 thì V biến M thành N
Nếu V biến (O) thành (O”) thì (O”) phải đi qua N
Vậy N là giao điểm của hai đường tròn (O’) và (O”)
Advertisements (Quảng cáo)
Từ đó suy ra cách dựng:
– Dựng O” = V(O)
– Gọi N = (O’) ∩ (O”), M = AN ∩ (O)
Câu 29. Cho đường tròn (O; R) và điểm I cố định khác O. Một điểm M thay đổi trên đường tròn. Tia phân giác của góc MOI cắt IM tại N. Tìm quỹ tích điểm N
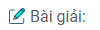
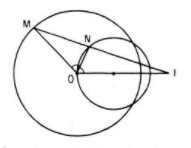
Đặt \(IO = d (d ≠ 0)\). Theo tính chất đường phân
giác của tam giác MOI, ta có:
\({{IN} \over {NM}} = {{IO} \over {OM}} = {d \over R}\)
Suy ra \({{IN} \over {IN + NM}} = {d \over {d + R}} \Leftrightarrow {{IN} \over {IM}} = {d \over {d + R}}\)
Vì hai vecto \(\overrightarrow {IN} \) và \(\overrightarrow {IM} \) cùng hướng nên đẳng
thức trên có nghĩa là:\(\overrightarrow {IN} = {d \over {d + R}}\overrightarrow {IM} \)
Nếu gọi V là phép vị tự tâm I tỉ số \(k = {d \over {d + R}}\) thì V biến điểm M thành điểm N
Khi M ở vị trí M0trên đường tròn (O ; R) sao cho \(\widehat {IO{M_0}} = {0^ \circ }\) thì tia phân giác của góc \(\widehat {IO{M_0}}\) không cắt IM. Điểm N không tồn tại.
Vậy khi M chạy trên (O ; R) (M khác hẳn M0) thì quỹ tích điểm N là ảnh của (O ; R) qua phép vị tự V bỏ đi ảnh của điểm M0
Câu 30. Cho hai đường tròn (O) và (O’) có bán kính khác nhau, tiếp xúc ngoài với nhau tại A. Một đường tròn (o”) thay đổi, luôn luôn tiếp xúc ngoài với (O) và (O’) lần lượt tại B và C . Chứng minh rằng đường thẳng BC luôn đi qua một điểm cố định
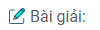
Kéo dài BC cắt (O’) tại B’
Vì C là tâm vị tự trong của (O’) và (O”) nên hai vecto \(\overrightarrow {O’B} \) và \(\overrightarrow {O”B’} \) ngược hướng
Vì B là tâm vị tự trong của (O) và (O”) nên hai vecto \(\overrightarrow {O”B} \) và \(\overrightarrow {OB} \) ngược hướng
Vậy hai vecto \(\overrightarrow {OB} \) và \(\overrightarrow {O’B’} \) cùng hướng
Từ đó suy ra đường thẳng BB’, cũng chính là đường thẳng BC, luôn đi qua điểm cố định là tâm vị tự ngoài I của (O) và (O’)

